

分析 (1)只要證明△ABE,△AEC是等腰三角形即可.
(2)如圖2中,當BD是特異線時,分三種情形討論,如圖3中,當AD是特異線時,AB=BD,AD=DC根據等腰三角形性質即可解決問題,當CD為特異線時,不合題意.
解答 (1)證明:如圖1中,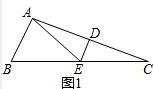
∵DE是線段AC的垂直平分線,
∴EA=EC,即△EAC是等腰三角形,
∴∠EAC=∠C,
∴∠AEB=∠EAC+∠C=2∠C,
∵∠B=2∠C,
∴∠AEB=∠B,即△EAB是等腰三角形,
∴AE是△ABC是一條特異線.
(2)解:如圖2中,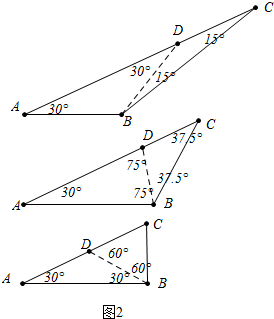
當BD是特異線時,如果AB=BD=DC,則∠ABC=∠ABD+∠DBC=120°+15°=135°,
如果AD=AB,DB=DC,則∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°,
如果AD=DB,DC=CB,則ABC=∠ABD+∠DBC=30°+60°=90°(不合題意舍棄).
如圖3中,當AD是特異線時,AB=BD,AD=DC,則∠ABC=180°-20°-20°=140°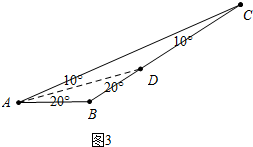
當CD為特異線時,不合題意.
∴符合條件的∠ABC的度數為135°或112.5°或140°.
點評 本題考查了等腰三角形的判定和性質、三角形內角和定理等知識,解題的關鍵是理解題意,學會分類討論,學會畫出圖形,借助于圖形解決問題,學會利用方程去思考問題,屬于中考創新題目.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在等邊△ABC中,點E、F分別在AB、BC邊上,且AE=BF=$\frac{1}{3}$AB,連接AF、CE交于點G,將△ABC沿AC翻折得到△ACD,連接DG,且DG=6$\sqrt{7}$,過點D作∠CDG的角平分線交CB于M,則四邊形DGFM的面積是77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$.
如圖,在等邊△ABC中,點E、F分別在AB、BC邊上,且AE=BF=$\frac{1}{3}$AB,連接AF、CE交于點G,將△ABC沿AC翻折得到△ACD,連接DG,且DG=6$\sqrt{7}$,過點D作∠CDG的角平分線交CB于M,則四邊形DGFM的面積是77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -(2a-b+c)=-2a-b+c | B. | -(x-y)+(xy-1)=-x+y+xy-1 | ||
| C. | -(3b-2c)=-3b-2c | D. | -[x-(5z+4)]=-x-5z+4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,矩形ABCD的頂點A與坐標原點O重合,B(4,0),D(0,3),點E從點A出發,沿射線AB移動,以CE為直徑作⊙M,點F為⊙M與射線DB的公共點,連接EF、CF,過點E作EG⊥EF,EG與⊙M相交于點G,連接CG.
如圖,在平面直角坐標系中,矩形ABCD的頂點A與坐標原點O重合,B(4,0),D(0,3),點E從點A出發,沿射線AB移動,以CE為直徑作⊙M,點F為⊙M與射線DB的公共點,連接EF、CF,過點E作EG⊥EF,EG與⊙M相交于點G,連接CG.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
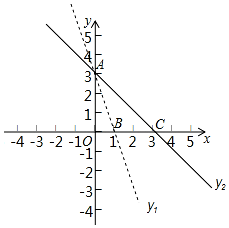 已知函數y1=k1x+b1和y2=k2x+b2圖象如圖所示,直線y1與直線y2交于A點(0,3).與x軸的交點坐標為B(1,0)、C(3,0).
已知函數y1=k1x+b1和y2=k2x+b2圖象如圖所示,直線y1與直線y2交于A點(0,3).與x軸的交點坐標為B(1,0)、C(3,0).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com