Question

13．如圖，在平面直角坐標系中，矩形ABCD的頂點A與坐標原點O重合，B（4，0），D（0，3），點E從點A出發，沿射線AB移動，以CE為直徑作⊙M，點F為⊙M與射線DB的公共點，連接EF、CF，過點E作EG⊥EF，EG與⊙M相交于點G，連接CG．
（1）試說明四邊形EFCG是矩形；
（2）求tan∠CEG的值；
（3）當⊙M與射線DB相切時，點E停止移動，在點E移動的過程中：
①點M運動的路徑長$\frac{25}{8}$；點G運動的路徑長$\frac{15}{4}$；
②矩形EFCG的面積最小值是$\frac{108}{25}$；
③當△BCG成為等腰三角形時，直接寫出點G坐標（$\frac{41}{8}$，$\frac{3}{2}$）．

Answer 1

分析 （1）根據三個角是直角的四邊形是矩形即可判斷．
（2）只要證明∠CEG=∠ADB即可解決問題；
（3）①根據圓周角定理和矩形的性質可證到∠GDC=∠FDE=定值，從而得到點G的移動的路線是線段，只需找到點G的起點與終點，求出該線段的長度即可；再判斷出M的移動路線是線段M'M''；
②欲求矩形EFCG面積的最小值，由題意可知當EC最小時，面積最小，求出EG、CG即可解決問題．
③先判斷出BG=CG時，點F是矩形ABCD的對角線BD中點，利用三角形的中位線求出FH，再用勾股定理計算即可．

解答 解：（1）證明：∵CE為⊙O的直徑，
∴∠CFE=∠CGE=90°，
∵EG⊥EF，
∴∠FEG=90°，
∴∠CFE=∠CGE=∠FEG=90°，
∴四邊形EFCG是矩形．

（2）由（1）知四邊形EFCG是矩形．
∴CF∥EG，
∴∠CEG=∠ECF，
∵∠ECF=∠EBF，
∴∠CEG=∠EBF，
在Rt△ABD中，AD=3，AB=4，
∴tan∠ABD=$\frac{AD}{AB}$，
∴tan∠CEG=$\frac{3}{4}$；

（3）①∵∠GBC=∠FBE=定值，點G的起點為B，終點為G″，如圖2所示，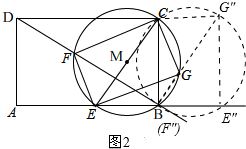

∴點G的移動路線是線段BG″，
∵∠G″BC=∠DBA，∠BCG″=∠A=90°，
∴△BCG″∽△BAD．
∴$\frac{BC}{AB}$=$\frac{BG″}{DB}$=$\frac{CG″}{AD}$．
∴$\frac{3}{4}$=$\frac{BG″}{5}$=$\frac{CG″}{3}$，
∴BG″=$\frac{15}{4}$，CG''=$\frac{9}{4}$，
∴點G移動路線的長為 $\frac{15}{4}$，
∵點M是以CE為直徑的圓的圓心，點M的起點是M'，終點是M''，如圖2-1所示，且M'M''∥AB，
∴點M的移動路線為線段M'M''，
∵點M'，M''是AC，CE''的中點，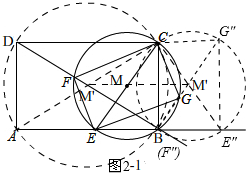

∴M'M''=$\frac{1}{2}$AB+$\frac{1}{2}$CG''=2+$\frac{9}{8}$=$\frac{25}{8}$，
點M運動的路徑長為$\frac{25}{8}$，
故答案分別為$\frac{25}{8}$，$\frac{15}{4}$．

②∵tan∠CEG=$\frac{3}{4}$，是定值，
∴∠CEG的大小不變，
∴CE最短時，矩形CFEG的面積最小，此時EC=3，
∴設CG=3k，EG=4k，則有25k²=9，
∴k=$\frac{3}{5}$，CG=$\frac{9}{5}$，EG=$\frac{12}{5}$，
∴矩形EFCG的面積最小值=CG•EG=$\frac{108}{25}$，
故答案為$\frac{108}{25}$．

③如圖3，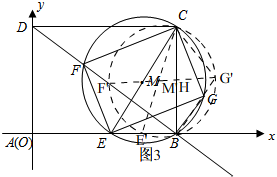
由運動知，點G始終是劣弧 $\widehat{BC}$上，
∵△BCG成為等腰三角形，
∴只有BG=CG，
∵四邊形E'F'CG'是矩形，
∴點F'是BD中點，
∵F'G'∥CD，
∴F'H=$\frac{1}{2}$AB=2，M'H=$\frac{1}{2}$BE'，
設⊙M'的半徑為r，則M'H=2-r，
∴BE'=2（2-r），
在Rt△BCE'中，CE'=2r，BC=3，
根據勾股定理得，（2r）²-[2（2-r）]²=9，
∴r=$\frac{25}{16}$，
∵F是BD中點，
∴F（2，$\frac{3}{2}$），
∴G'（2+2×$\frac{25}{16}$，$\frac{3}{2}$），
∴G'（ $\frac{41}{8}$，$\frac{3}{2}$）．
故答案為（$\frac{41}{8}$，$\frac{3}{2}$）．

點評 此題是圓的綜合題，主要考查考查了矩形的判定與性質、相似三角形的判定與性質、圓周角定理、直角三角形斜邊上的中線等于斜邊的一半、垂線段定理等知識，考查了動點的移動的路線長，綜合性較強．而發現∠CBG=∠ABD及∠FCE=∠ABD是解決本題的關鍵．判斷出點F是線段BD中點是難點．