Question

6．在△ABC中，點D在BC邊上，且滿足CA²=CD•CB（如圖1）
（1）求證：$\frac{AD}{AB}$=$\frac{AC}{BC}$；
（2）如圖2，以點A為圓心，AB為半徑畫弧交AC的延長線于點E，聯結BE，延長AD交BE于點F，求證：$\frac{EF}{BF}$=$\frac{AD}{BD}$

Answer 1

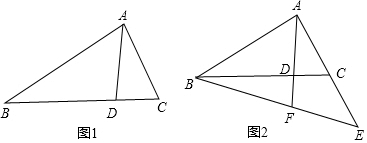
分析 （1）由CA²=CD•CB知CA：CD=CB：CA，根據∠C=∠C證△CAB∽△CDA即可得；
（2）過點B作BG∥AE，交AF的延長線于點G，由△ACD∽△BCA知∠CAD=∠CBA，結合BG∥AE，即∠G=∠CAD，得∠G=∠CBA，證△ABD∽△AGB得$\frac{AB}{GB}=\frac{AD}{BD}$，由BG∥AE知$\frac{EF}{BF}$=$\frac{AE}{GB}$=$\frac{AB}{GB}$，從而得證$\frac{EF}{BF}$=$\frac{AD}{BD}$．

解答 證明：（1）∵CA²=CD•CB，
∴CA：CD=CB：CA
∵∠C=∠C，
∴△CAB∽△CDA，
∴$\frac{AD}{AB}$=$\frac{AC}{BC}$；

（2）如圖，過點B作BG∥AE，交AF的延長線于點G，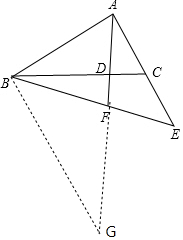

∵△ACD∽△BCA，
∴∠CAD=∠CBA，
∵BG∥AE，
∴∠G=∠CAD，
∴∠G=∠CBA，
又∠BAD=∠GAB，
∴△ABD∽△AGB，
∴$\frac{AD}{AB}$=$\frac{BD}{GB}$，即$\frac{AB}{GB}=\frac{AD}{BD}$，
∵BG∥AE，
∴$\frac{EF}{BF}$=$\frac{AE}{GB}$，
又∵AE=AB，
∴$\frac{EF}{BF}$=$\frac{AB}{GB}$，
∴$\frac{EF}{BF}$=$\frac{AD}{BD}$．

點評 本題主要考查相似三角形的判定與性質，通過構建△ABD∽△AGB將$\frac{EF}{BF}$與$\frac{AD}{BD}$通過$\frac{AE}{BG}$聯系到一起是解題的關鍵．