
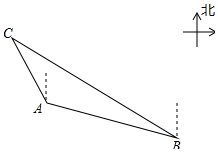
 如圖,一艘海上巡邏船在A地巡航,這時接到B地海上指揮中心緊急通知:在指揮中心北偏西60°向的C地,有一艘漁船遇險,要求馬上前去救援.此時C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B兩地之間的距離為16海里.求A、C兩地之間的距離.(保留根號)
如圖,一艘海上巡邏船在A地巡航,這時接到B地海上指揮中心緊急通知:在指揮中心北偏西60°向的C地,有一艘漁船遇險,要求馬上前去救援.此時C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B兩地之間的距離為16海里.求A、C兩地之間的距離.(保留根號) 分析 過點B作BD⊥CA交CA延長線于點D,根據題意可得∠ACB和∠ABC的度數,然后根據三角形外角定理求出∠DAB的度數,已知AB=12海里,可求出BD、AD的長度,在Rt△CBD中,解直角三角形求出CD的長度,繼而可求出A、C之間的距離.
解答 解:過點B作BD⊥CA交CA延長線于點D,
由題意得,∠ACB=60°-30°=30°,
∠ABC=75°-60°=15°,
∴∠DAB=∠DBA=45°,
在Rt△ABD中,AB=16海里,∠DAB=45°,
∴BD=AD=ABcos45°=8$\sqrt{2}$(海里),
在Rt△CBD中,CD=$\frac{BD}{tan30°}$=8$\sqrt{6}$,
∴AC=(8$\sqrt{6}$-8$\sqrt{2}$)(海里),
答:A、C兩地之間的距離是8($\sqrt{6}$-$\sqrt{2}$)海里.
點評 本題考查了解直角三角形的知識,解答本題的關鍵是構造直角三角形,利用三角函數的知識求解相關線段的長度,難度一般.


 全能練考卷系列答案
全能練考卷系列答案科目:初中數學 來源: 題型:解答題
 如圖在△ABC中,AD⊥BC于D點,正方形EFGH的一邊FG在BC上,頂點E,H分別在AB,AC上,BC=40cm,AD=30cm
如圖在△ABC中,AD⊥BC于D點,正方形EFGH的一邊FG在BC上,頂點E,H分別在AB,AC上,BC=40cm,AD=30cm查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
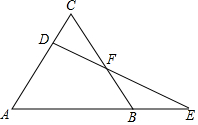 如圖,已知△ABC是等邊三角形,D為AC邊上的一個動點,延長AB到E,使BE=CD,連結DE交BC于F.
如圖,已知△ABC是等邊三角形,D為AC邊上的一個動點,延長AB到E,使BE=CD,連結DE交BC于F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com