
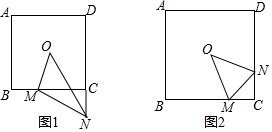
分析 (1)結(jié)論:MN=BM+CN.在CD上取一點(diǎn)G,使得CG=BM,只要證明△OBM≌△OCG,△ONM≌△ONG即可解決問(wèn)題.
(2)結(jié)論:MN=BM-CN.在CD上取一點(diǎn)G,使得CG=BM,只要證明△OBM≌△OCG,△ONM≌△ONG即可解決問(wèn)題.
(3)設(shè)CN=x,由CM=1,BC=4,推出BM=3.由BM=CN+MN,推出MN=3-x,在Rt△MNC中,根據(jù)MN2=CN2+CM2,列出方程即可解決問(wèn)題.
解答 解:(1)結(jié)論:MN=BM+CN.
理由:在CD上取一點(diǎn)G,使得CG=BM.
在△OBM和△OCG中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBM=∠OCG}\\{BM=CG}\end{array}\right.$,
∴△OBM≌△OCG,
∴OM=OG,∠BOM=∠COG,
∵∠MON=45°,∠BOC=90°,
∴∠BOM+∠CON=∠CON+∠COG=45°,
∴∠NOM=∠NOG=45°,∵ON=ON,
∴△ONM≌△ONG,
∴NM=GN,
∵NG=CN+CG=CN+BM,
∴MN=BM+CN.
(2)結(jié)論:MN=BM-CN.
理由:在CD上取一點(diǎn)G,使得CG=BM.
在△OBM和△OCG中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBM=∠OCG}\\{BM=CG}\end{array}\right.$,
∴△OBM≌△OCG,
∴OM=OG,∠BOM=∠COG,
∴∠BOC=∠MOG=90°
∴∠NOM=45°,
∴∠NOG=45°
∴∠NOM=∠NOG,∵ON=ON,
∴△ONM≌△ONG,
∴NM=GN,
∵NG=CG-CN=BM-CN,
∴MN=BM-CN.
(3)設(shè)CN=x,
∵CM=1,BC=4,
∴BM=3.
∵BM=CN+MN,
∴MN=3-x,
在Rt△MNC中,∵M(jìn)N2=CN2+CM2,
∴(3-x)2=x2+12,
∴x=$\frac{4}{3}$,
∴CN=$\frac{4}{3}$
點(diǎn)評(píng) 本題考查正方形的性質(zhì)、全等三角形的判定和性質(zhì)等知識(shí),解題的關(guān)鍵是學(xué)會(huì)添加常用輔助線,構(gòu)造全等三角形解決問(wèn)題,學(xué)會(huì)用方程的思想思考問(wèn)題,屬于中考常考題型.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $-\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-|{\frac{3}{4}}|$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
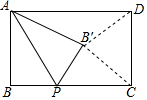 如圖,在矩形ABCD中,AB=a,BC=b,點(diǎn)P是BC上的一個(gè)動(dòng)點(diǎn),連接AP,把△PAB沿著AP翻折到△PB′C(點(diǎn)B′在矩形的內(nèi)部),連接B′C,B′D.點(diǎn)P在整個(gè)運(yùn)動(dòng)過(guò)程中,若存在唯一的位置使得△B′CD為直角三角形,則a,b之間的數(shù)量關(guān)系是b=$\sqrt{2}$a.
如圖,在矩形ABCD中,AB=a,BC=b,點(diǎn)P是BC上的一個(gè)動(dòng)點(diǎn),連接AP,把△PAB沿著AP翻折到△PB′C(點(diǎn)B′在矩形的內(nèi)部),連接B′C,B′D.點(diǎn)P在整個(gè)運(yùn)動(dòng)過(guò)程中,若存在唯一的位置使得△B′CD為直角三角形,則a,b之間的數(shù)量關(guān)系是b=$\sqrt{2}$a.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 361×106 | B. | 36.1×107 | C. | 3.61×108 | D. | 3.61×109 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
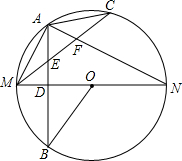 如圖所示,MN是⊙O的直徑,作AB⊥MN,垂足為點(diǎn)D,連接AM,AN,點(diǎn)C為弧AN上一點(diǎn),且$\widehat{AC}$=$\widehat{AM}$,連接CM,交AB于點(diǎn)E,交AN于點(diǎn)F,現(xiàn)給出以下結(jié)論:①M(fèi)D=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正確的結(jié)論有②③④.(請(qǐng)把所有正確結(jié)論的序號(hào)都填在橫線上)
如圖所示,MN是⊙O的直徑,作AB⊥MN,垂足為點(diǎn)D,連接AM,AN,點(diǎn)C為弧AN上一點(diǎn),且$\widehat{AC}$=$\widehat{AM}$,連接CM,交AB于點(diǎn)E,交AN于點(diǎn)F,現(xiàn)給出以下結(jié)論:①M(fèi)D=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正確的結(jié)論有②③④.(請(qǐng)把所有正確結(jié)論的序號(hào)都填在橫線上)查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com