Question

14．己知AD∥CE，點B為直線AD、CE所確定的平面內一點．
（1）如圖1所示，求證：∠ADB=∠B+∠BFE．
（2）如圖2，FG平分∠BFE，DG交FG于點G交BF于點H，且∠BDG：∠ADG=2：1，∠B=20°，∠DGF=30°，求∠BHD的度數．

Answer 1

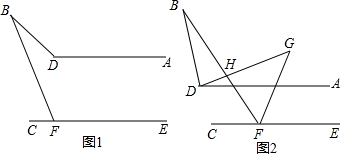
分析 （1）先延長BD交EF于N，根據平行線的性質以及∠BNE是△BFN的外角，可求得∠ADB=∠B+∠BFE；
（2）延長BD交FE于M，設∠BDG=α，根據AD∥FE，得出∠ADB=∠EMB=$\frac{3}{2}$α，再根據三角形內角和定理以及角平分線的定義，求得∠BFE=2α-20°，最后根據∠BFE是△BMF的外角，可得∠BFE=∠B+∠BME，得到2α-20°=20°+$\frac{3}{2}$α，求得∠BDH=80°，即可得到∠BHD=180°-20°-80°=80°．

解答 解：（1）如圖1，延長BD交EF于N，
∵AD∥CE，
∴∠ADB=∠ENB，
∵∠BNE是△BFN的外角，
∴∠BNE=∠B+∠BFE，
∴∠ADB=∠B+∠BFE；

（2）如圖2，延長BD交FE于M，設∠BDG=α，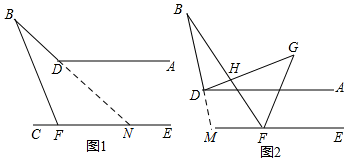
∵∠BDG：∠ADG=2：1，
∴∠ADB=α+$\frac{1}{2}$α=$\frac{3}{2}$α，
∵AD∥FE，
∴∠ADB=∠EMB=$\frac{3}{2}$α，
∵DG交BF于點H，∠B=20°，∠DGF=30°，
∴∠BFG=α-10°，
∵FG平分∠BFE，
∴∠BFE=2α-20°，
∵∠BFE是△BMF的外角，
∴∠BFE=∠B+∠BME，
即2α-20°=20°+$\frac{3}{2}$α，
解得α=80°，
∴∠BDH=80°，
∴△BDH中，∠BHD=180°-20°-80°=80°．

點評 本題主要考查了平行線的性質、三角形內角和定理以及三角形外角性質的綜合應用，解決問題的關鍵是作輔助線構造三角形，運用三角形的一個外角等于和它不相鄰的兩個內角的和進行計算．