
【題目】科技驅動新零售商業變革的時代已經來臨,無人超市的經營模式已在全國各地興起,某家無人超市開業以來,經測算,為銷售A型商品每天需固定支出的費用為400元,若A型商品每件的銷售利潤不超過9元,每天銷售A型商品的數量為280件,若A型商品每件的銷售利潤超過9元,則每超過1元,每天銷售A型商品的數量減少10件,設該家無人超市A型商品的銷售利潤為x元/件,A型商品的日凈收入為y元(日凈收入=A型商品每天銷售的總利潤﹣A型商品每天固定的支出費用):
(1)試求出該超市A型商品的日凈收入為y(元)與A型商品的銷售利潤x(元/件)之間的關系式;
(2)該超市能否實現A型商品的銷售日凈收入3000元的目的?如能實現,求出A型商品的銷售利潤為多少元/件?如不能實現,請說明理由;
(3)請問該超市A型商品的銷售利潤為多少元/件時,能獲得A型商品的最大日凈收入?
【答案】(1)![]() ;(2)該超市能實現A型商品的銷售日凈收入3000元的目的,A型商品的銷售利潤為17元/件或20元/件;(3)該超市A型商品的銷售利潤為18元/件或19元/件時,能獲得A型商品的最大日凈收入.
;(2)該超市能實現A型商品的銷售日凈收入3000元的目的,A型商品的銷售利潤為17元/件或20元/件;(3)該超市A型商品的銷售利潤為18元/件或19元/件時,能獲得A型商品的最大日凈收入.
【解析】
(1)根據題意可以列出相應的函數解析式;
(2)根據(1)中的函數解析式即可解答本題;
(3)根據(1)中的函數解析式即可求得y的最大值.
解:(1)由題意可得,
當0<x≤9時,y=280x﹣400,
當x>9時,y=[280﹣(x﹣9)×10]x﹣400=﹣10x2+370x﹣400,
由上可得,該超市A型商品的日凈收入為y(元)與A型商品的銷售利潤x(元/件)之間的關系式是:y=![]() ;
;
(2)∵當0<x≤9時,y=280x﹣400≤2120,
∴令y=3000代入y=﹣10x2+370x﹣400,
解得,x1=17,x2=20,
答:該超市能實現A型商品的銷售日凈收入3000元的目的,A型商品的銷售利潤為17元/件或20元/件;
(3)∵當0<x≤9時,y=280x﹣400≤2120,
當x>9時,y=﹣10x2+370x﹣400=﹣10(x﹣![]() )2+3022.5,
)2+3022.5,
∵x>9且x為整數,
∴當x=18或19時,y取得最大值,此時y=3020,
答:該超市A型商品的銷售利潤為18元/件或19元/件時,能獲得A型商品的最大日凈收入.


科目:初中數學 來源: 題型:
【題目】已知,PA、PB是⊙O的切線,切點分別為A、B,AC是⊙O的直徑.
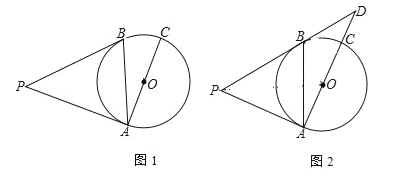
(1)如圖1,若∠BAC=25°,求∠P的度數;
(2)如圖2,延長PB、AC相交于點D.若AP=AC,求cosD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強學生的安全意識,某校組織了學生參加安全知識競賽,從中抽取了部分學生成績(得分數取正整數,滿分為100分)進行統計,繪制統計圖如下(未完成),解答下列問題:


(1)若A組的頻數比B組小24,求頻數分布直方圖中的![]() 、
、![]() 的值;
的值;
(2)扇形統計圖中,D部分所對的圓心角為n°,求n的值并補全頻數分布直方圖;
(3)若成績在80分以上為優秀,全校共有2000名學生,估計成績優異的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校有3000名學生.為了解全校學生的上學方式,該校數學興趣小組以問卷調查的形式,隨機調查了該校部分學生的主要上學方式(參與問卷調查的學生只能從以下六個種類中選擇一類),并將調查結果繪制成如下不完整的統計圖.
種類 | A | B | C | D | E | F |
上學方式 | 電動車 | 私家車 | 公共交通 | 自行車 | 步行 | 其他 |
某校部分學生主要上學方式扇形統計圖某校部分學生主要上學方式條形統計圖
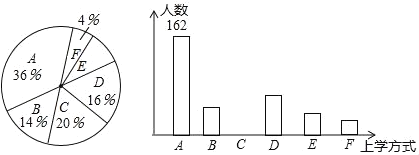
根據以上信息,回答下列問題:
(1)參與本次問卷調查的學生共有____人,其中選擇B類的人數有____人.
(2)在扇形統計圖中,求E類對應的扇形圓心角α的度數,并補全條形統計圖.
(3)若將A、C、D、E這四類上學方式視為“綠色出行”,請估計該校每天“綠色出行”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點E為正方形ABCD的邊CD上一點,DF⊥AE于點F,交AC于點M,交BC于點G,在CD上取一點G′,使CG′=CG.連接MG′.

(1)求證:∠AED=∠CG′M;
(2)如圖2,連接BD交AE于點N,連接MN,MG′交AE于H.
①試判斷MN與CD的位置關系,并說明理由;
②若AB=12,DG′=G′E,求AH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,M為等腰三角形ABD的底邊AB的中點,過D作DC∥AB,連接BC,AB=6cm,DM=3cm,DC=3-![]() cm.動點P自A點出發,在AB上勻速運動,動點Q自點B出發,在折線BC-CD上勻速運動,速度均為1cm/s,兩點同時出發,當其中一個動點到達終點時,它們同時停止運動,設點P運動t(s)時,△MPQ的面積為S.
cm.動點P自A點出發,在AB上勻速運動,動點Q自點B出發,在折線BC-CD上勻速運動,速度均為1cm/s,兩點同時出發,當其中一個動點到達終點時,它們同時停止運動,設點P運動t(s)時,△MPQ的面積為S.
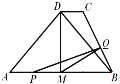
(1)當點P在線段AM上運動時,PM=_______.(用t的代數式表示)
(2)求BC的長度;
(3)當點P在MB上運動時,求S與t之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某足球運動員站在點O處練習射門,將足球從離地面0.5m的A處正對球門踢出(點A在y軸上),足球的飛行高度y(單位:m)與飛行時間t(單位:s)之間滿足函數關系y=at2+5t+c,已知足球飛行0.8s時,離地面的高度為3.5m.
(1)足球飛行的時間是多少時,足球離地面最高?最大高度是多少?
(2)若足球飛行的水平距離x(單位:m)與飛行時間t(單位:s)之間具有函數關系x=10t,已知球門的高度為2.44m,如果該運動員正對球門射門時,離球門的水平距離為28m,他能否將球直接射入球門?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線m:y=ax2+b(a<0,b>0)與x軸于點A、B(點A在點B的左側),與y軸交于點C.將拋物線m繞點B旋轉180°,得到新的拋物線n,它的頂點為C1,與x軸的另一個交點為A1.若四邊形AC1A1C為矩形,則a,b應滿足的關系式為( )
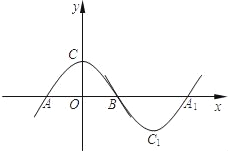
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com