
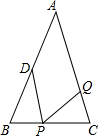
 如圖,在△ABC中,AB=AC=28cm,BC=20cm,點D是AB邊的中點,若有一動點P在BC邊上由點B向點C運動,點Q在CA邊上由點C向A運動.
如圖,在△ABC中,AB=AC=28cm,BC=20cm,點D是AB邊的中點,若有一動點P在BC邊上由點B向點C運動,點Q在CA邊上由點C向A運動.分析 (1)根據SAS證明△BPD≌△CPQ,可得出答案;
(2)根據全等三角形應滿足的條件探求邊之間的關系,再根據路程=速度×時間公式,先求得BP,CQ,PC,若△BPD≌△CPQ必須有BP=CP,可得方程求解即可.
解答 解:(1)△BPD≌△CPQ,
∵D是AB的中點,
∴BD=14.
又∵BP=3×2=6,
∴CP=20-6=14,CQ=3×2=6,
∵AB=AC,
∴∠B=∠C,
在△BPD和△CPQ中,
$\left\{\begin{array}{l}{BD=CP}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$,
∴△BPD≌△CPQ.
(2)存在,設經過t秒時△BPD≌△CPQ.
依題意BP=2.5t,CQ=3.5t,PC=20-2.5t.
若△BPD≌△CPQ必須有BP=CP,即2.5t=20-2.5t,
解得t=4.
故當t=4秒時△BPD≌△CPQ.
點評 此題考查了勾股定理,全等三角形的判定,主要運用了路程=速度×時間的公式,要求熟練運用全等三角形的判定和性質.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
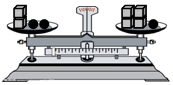 如圖,一個平衡的天平盤中,左盤有2個小正方體和2個小球,右盤有4個小正方體和1個小球.每個小球的重量用x克表示,小正方體每個5克,那么可列方程得2×5+2x=4×5+x.
如圖,一個平衡的天平盤中,左盤有2個小正方體和2個小球,右盤有4個小正方體和1個小球.每個小球的重量用x克表示,小正方體每個5克,那么可列方程得2×5+2x=4×5+x.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com