
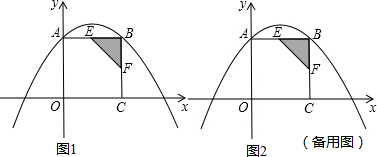
分析 (1)根據(jù)點A、B的坐標和3a-b=1利用待定系數(shù)法即可求出二次函數(shù)的解析式;
(2)①運動開始t秒時,EB=6-t,BF=t,根據(jù)三角形的面積公式即可得出S關于t的函數(shù)關系式,利用配方法即可得出最值問題;
②假設存在,結合①可得出點E、F的坐標,分別以BE、BF、EF為對角線根據(jù)平行四邊形的性質(zhì)求出點R的坐標,再由點R在拋物線上利用二次函數(shù)圖象上的坐標特征確定點R的坐標,此題得解.
解答 解:(1)已知點A(0,6),B(6,6)在拋物線上,且3a-b=-1,
∴$\left\{\begin{array}{l}{6=c}\\{6=36a+6b+c}\\{3a-b=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{9}}\\{b=\frac{2}{3}}\\{c=6}\end{array}\right.$,
∴二次函數(shù)的解析式為y=-$\frac{1}{9}$x2+$\frac{2}{3}$x+6.
(2)①運動開始t秒時,EB=6-t,BF=t,
S=$\frac{1}{2}$BE•BF=$\frac{1}{2}$(6-t)t=-$\frac{1}{2}$t2+3t=-$\frac{1}{2}$(t-3)2+$\frac{9}{2}$.
當t=3時,S有最大值$\frac{9}{2}$.
②假設存在,當S取得最大值時,由①知t=3,
∴點E(3,6),點F(6,3).
以E、B、R、F為頂點的四邊形是平行四邊形分三種情況(如圖):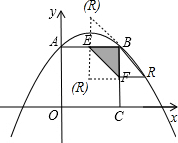
(i)以BE為對角線時,
∵點B(6,6),點E(3,6),點F(6,3),
∴點R(6+3-6,6+6-3),即(3,9);
(ii)以BF為對角線時,
∵點B(6,6),點E(3,6),點F(6,3),
∴點R(6+6-3,6+3-6),即(9,3);
(iii)以EF為對角線時,
∵點B(6,6),點E(3,6),點F(6,3),
∴點R(6+3-6,6+3-6),即(3,3).
∵點R在拋物線y=-$\frac{1}{9}$x2+$\frac{2}{3}$x+6上,
∴點R的坐標為(9,3).
故拋物線上存在點R(9,3),使得四邊形EBRF為平行四邊形.
點評 本題考查了待定系數(shù)法求函數(shù)解析式、三角形的面積公式、二次函數(shù)的性質(zhì)以及平行四邊形的性質(zhì),解題的關鍵是:(1)利用待定系數(shù)法求出函數(shù)解析式;(2)①根據(jù)三角形的面積公式找出S關于t的函數(shù)關系式;②利用平行四邊形的性質(zhì)求出點R的坐標.本題屬于中檔題,難度不大,解決該題型題目時,根據(jù)平行線的性質(zhì)對角線互相平分結合三個頂點的坐標求出第四個頂點的坐標是關鍵.


 全優(yōu)考典單元檢測卷及歸類總復習系列答案
全優(yōu)考典單元檢測卷及歸類總復習系列答案科目:初中數(shù)學 來源: 題型:解答題
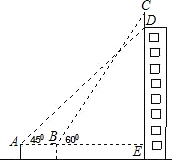 如圖某幢大樓頂部有一廣告牌CD,甲、乙兩人分別在相距8米的A、B兩處測得D點和C點的仰角分別為45°和60°,且A、B、E三點在一直線(∠AEC=90°)上,若BE=15米,求這塊廣告牌的CD.(取 $\sqrt{3}$=1.73,計算結果保留整數(shù))
如圖某幢大樓頂部有一廣告牌CD,甲、乙兩人分別在相距8米的A、B兩處測得D點和C點的仰角分別為45°和60°,且A、B、E三點在一直線(∠AEC=90°)上,若BE=15米,求這塊廣告牌的CD.(取 $\sqrt{3}$=1.73,計算結果保留整數(shù))查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 擴大為原來的4倍 | B. | 擴大為原來的2倍 | C. | 不變 | D. | 縮小為原來的$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知,在平面直角坐標系中,A(-3,-4),B(0,-2).
如圖,已知,在平面直角坐標系中,A(-3,-4),B(0,-2).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
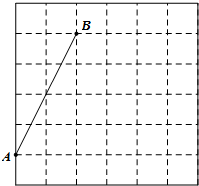 如圖,在每個小正方形的邊長均為1的方格紙中,有線段AB,點A、B均在小正方形的頂點上.
如圖,在每個小正方形的邊長均為1的方格紙中,有線段AB,點A、B均在小正方形的頂點上.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com