
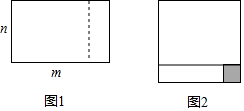
 如圖1,把一個長為m、寬為n的長方形(m>n),沿虛線剪開,將其與陰影部分所表示的小正方形一起拼接成如圖2所示的長方形,則下列說法不正確的是( )
如圖1,把一個長為m、寬為n的長方形(m>n),沿虛線剪開,將其與陰影部分所表示的小正方形一起拼接成如圖2所示的長方形,則下列說法不正確的是( )| A. | 圖2所示的長方形是正方形 | |
| B. | 圖2所示的長方形周長=2m+2n | |
| C. | 陰影部分所表示的小正方形邊長=m-n | |
| D. | 陰影部分所表示的小正方形面積=$\frac{(m-n)^{2}}{4}$ |
分析 設小正方形的邊長為a,C、根據圖形的拼法可得出關于a的一元一次方程,解之即可用含m、n的代數式表示出a的值,由此得出C選項不符合題意;A、觀察圖形2找出圖形2中長方形的相鄰兩邊長,由此可得出該長方形為正方形,即A選項符合題意;B、根據正方形的周長公式即可找出圖形2的周長,再代入a值即可得知B選項符合題意;D、根據正方形的面積公式,再代入a值,即可得知D選項符合題意.綜上即可得出結論.
解答 解:設小正方形的邊長為a,
C、根據圖形的拼法可知:m-a=n+a,
∴a=$\frac{m-n}{2}$,
∴C選項不符合題意;
A、∵圖2中長方形相鄰兩邊長度分別為n+a,n+a,
∴圖2所示的長方形是正方形,
∴A選項符合題意;
B、∵圖2所示的長方形周長=4(n+a)=4(n+$\frac{m-n}{2}$)=4×$\frac{m+n}{2}$=2m+2n,
∴B選項符合題意;
D、∵陰影部分所表示的小正方形面積=a2=$(\frac{m-n}{2})^{2}$=$\frac{(m-n)^{2}}{4}$,
∴D選項符合題意.
故選C.
點評 本題考查了完全平方公式的幾何背景、正方形的周長及面積,根據圖形的拼法找出小正方形的邊長,再逐一分析四個選項的正誤是解題的關鍵.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:選擇題
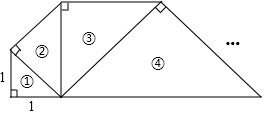 如圖,一系列等腰直角三角形(編號分別為①、②、③、④、…)組成了一個螺旋形,其中第1個三角形的直角邊長為1,則第n個等腰直角三角形的面積為( )
如圖,一系列等腰直角三角形(編號分別為①、②、③、④、…)組成了一個螺旋形,其中第1個三角形的直角邊長為1,則第n個等腰直角三角形的面積為( )| A. | 2n-3 | B. | 2n-2 | C. | 2n-1 | D. | 2n |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
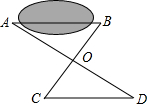 要測量池塘的寬度AB,畫出如圖所示的兩個三角形,下面測出的哪組條件不能使CD=AB( )
要測量池塘的寬度AB,畫出如圖所示的兩個三角形,下面測出的哪組條件不能使CD=AB( )| A. | OA=OD,OB=OC | B. | ∠B=∠C,OB=OC | C. | ∠B=∠C,OA=OD | D. | ∠C=∠B,∠A=∠D |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{6}{5}$小時 | B. | $\frac{5}{6}$小時 | C. | 2小時 | D. | 3小時 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知:如圖,在△ABC中,∠ACB=90°,CD是邊AB上的高,∠A=30°,則線段AB與BD的數量關系是( )
已知:如圖,在△ABC中,∠ACB=90°,CD是邊AB上的高,∠A=30°,則線段AB與BD的數量關系是( )| A. | AB=2BD | B. | AB=3BD | C. | AB=4BD | D. | AB=5BD |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com