
 如圖,拋物線y=ax2+bx-4a經(jīng)過A(-1,0),C(0,4)兩點(diǎn),與x軸交于另一點(diǎn)B.
如圖,拋物線y=ax2+bx-4a經(jīng)過A(-1,0),C(0,4)兩點(diǎn),與x軸交于另一點(diǎn)B.分析 (1)將A、C兩點(diǎn)的坐標(biāo)代入解析式中即可求出a與b的值.
(2)根據(jù)解析式求出點(diǎn)D的坐標(biāo),過點(diǎn)D作DE⊥x軸于點(diǎn)E,求出DE,OE、BE、OC和OE的長度,然后根據(jù)梯形面積和三角形面積即可求出答案.
解答 解:(1)將A(-1,0)、C(0,4)代入y=ax2+bx-4a,
∴$\left\{\begin{array}{l}{0=a-b-4a}\\{4=-4a}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$
∴拋物線的解析式為:y=-x2+3x+4
(2)由(1)可知:y=-(x-$\frac{3}{2}$)2+$\frac{25}{4}$
∴D($\frac{3}{2}$,$\frac{25}{4}$),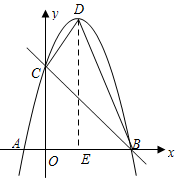
令y=0代入y=-x2+3x+4,
∴x=-1或x=4,
∴B(4,0)
∴DE=$\frac{25}{4}$,AE=$\frac{3}{2}$,BE=$\frac{5}{2}$,OC=4,OE=$\frac{3}{2}$
∴梯形OCDE的面積為:$\frac{1}{2}$(DE+OC)•OE=$\frac{123}{16}$,
△DEB的面積為:$\frac{1}{2}$BE•DE=$\frac{125}{16}$,
∴四邊形OCDB的面積為:$\frac{123}{16}$+$\frac{125}{16}$=$\frac{31}{2}$
點(diǎn)評 本題考查二次函數(shù)的綜合問題,解題的關(guān)鍵是根據(jù)條件求出二次函數(shù)的解析式,然后求出相關(guān)線段的出長度后,根據(jù)梯形面積和三角形面積即可求出答案.本題屬于中等題型.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
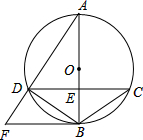 如圖,⊙O的直徑AB與弦CD交于點(diǎn)E,CE=DE,⊙O的切線BF與弦AD的延長線相交于點(diǎn)F.
如圖,⊙O的直徑AB與弦CD交于點(diǎn)E,CE=DE,⊙O的切線BF與弦AD的延長線相交于點(diǎn)F.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| 最高氣溫(℃) | 22 | 23 | 24 | 25 |
| 天數(shù) | 1 | 2 | 2 | 4 |
| A. | 25,24 | B. | 24.5,25 | C. | 24,25 | D. | 23.5,24 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
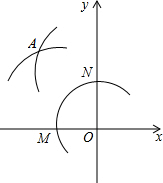 在平面直角坐標(biāo)系中,在x軸的負(fù)半軸與y軸的正半軸上分別截取OM,ON,使OM=ON;再分別以點(diǎn)M,N為圓心、大于$\frac{1}{2}$MN長為半徑作弧,兩弧在第二象限交于點(diǎn)A,若點(diǎn)A的坐標(biāo)為($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求點(diǎn)A的坐標(biāo).
在平面直角坐標(biāo)系中,在x軸的負(fù)半軸與y軸的正半軸上分別截取OM,ON,使OM=ON;再分別以點(diǎn)M,N為圓心、大于$\frac{1}{2}$MN長為半徑作弧,兩弧在第二象限交于點(diǎn)A,若點(diǎn)A的坐標(biāo)為($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求點(diǎn)A的坐標(biāo).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 已知線段AB=4cm,過點(diǎn)B作BC⊥AB,且BC=2cm,連結(jié)AC,以C為圓心,CB為半徑作弧,交AC于D;以A為圓心,AD為半徑作弧,交AB于P,量一量線段AP的長,約為( )
已知線段AB=4cm,過點(diǎn)B作BC⊥AB,且BC=2cm,連結(jié)AC,以C為圓心,CB為半徑作弧,交AC于D;以A為圓心,AD為半徑作弧,交AB于P,量一量線段AP的長,約為( )| A. | 2cm | B. | 2.5cm | C. | 3cm | D. | 3.5cm |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com