
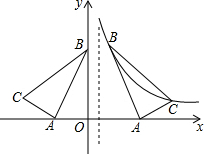
 如圖,在平面直角坐標系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),點C在第二象限且tan∠ACB=2,將Rt△ABC沿平行于y軸的某條直線翻折,得Rt△A1B1C1,若點B1,C1恰好落在反比例函數y=$\frac{k}{x}$(x>0)的圖象上,則k的值等于$\frac{16}{3}$.
如圖,在平面直角坐標系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),點C在第二象限且tan∠ACB=2,將Rt△ABC沿平行于y軸的某條直線翻折,得Rt△A1B1C1,若點B1,C1恰好落在反比例函數y=$\frac{k}{x}$(x>0)的圖象上,則k的值等于$\frac{16}{3}$. 分析 作CN⊥x軸于點N,易證△CAN∽△AOB,即可求出C的坐標,設平行于y軸的直線為x=c,用c表示出C1和B1,根據兩點都在反比例函數圖象上,進而求出c的值,即可求出求出k的值.
解答 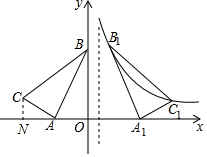 解:作CN⊥x軸于點N,
解:作CN⊥x軸于點N,
∵A(-2,0)B(0,4).
∴OB=4,AO=2,
易證△CAN∽△AOB,
∴$\frac{AN}{OB}$=$\frac{CN}{OA}$=$\frac{AC}{AB}$,
∵tan∠ACB=2,tan∠ACB=$\frac{AB}{AC}$,
∴$\frac{AN}{4}$=$\frac{CN}{2}$=$\frac{1}{2}$,
∴AN=2,CN=1,NO=NA+AO=4,
又∵點C在第二象限,
∴C(-4,1);
設平行于y軸的直線為x=c,
則C1(4+2c,1),B1(2c,4)
又點C1和B1在該比例函數圖象上,
∴4+2c=8c,
解得c=$\frac{2}{3}$,
∴k=2×$\frac{2}{3}$×4=$\frac{16}{3}$,
故答案為$\frac{16}{3}$.
點評 本題主要考查了反比例函數圖象上點點坐標特征,解直角三角形以及軸對稱的性質,解答本題的關鍵是熟練掌握反比例函數的性質以及軸對稱的性質,此題難度不是很大.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 單項式-x的次數和系數都是0 | |
| B. | -2016是整式 | |
| C. | -$\frac{{a}^{2}{b}^{\;}}{3}$的系數是-3 | |
| D. | 多項式2x2y3-3x3y3-1是五次三項式 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com