
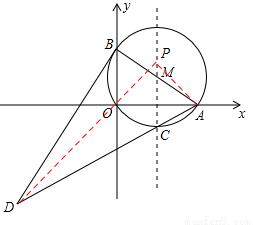
如圖,在平面直角坐標系中,⊙M過原點O,與x軸交于A(4,0),與y軸交于B(0,3),點C為劣弧AO的中點,連接AC并延長到D,使DC=4CA,連接BD.
(1)求⊙M的半徑;
(2)證明:BD為⊙M的切線;
(3)在直線MC上找一點P,使|DP﹣AP|最大.

(1)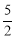 ;(2)證明見解析;(3)取點A關于直線MC的對稱點O,連接DO并延長交直線MC于P,此P點為所求,且線段DO的長為|DP﹣AP|的最大值,為
;(2)證明見解析;(3)取點A關于直線MC的對稱點O,連接DO并延長交直線MC于P,此P點為所求,且線段DO的長為|DP﹣AP|的最大值,為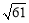 .
.
【解析】
試題分析:(1)利用A,B點坐標得出AO,BO的長,進而得出AB的長,即可得出圓的半徑.
(2)根據B,D 兩點求出直線BD表達式,求出BD與與 x 軸交點Q的坐標,從而求出AB,QA,BQ的長,根據勾股定理逆定理得出BD⊥AB,求出BD為⊙M的切線.
(3)取點A關于直線MC的對稱點O,連接DO并延長交直線MC于P,此P點為所求,且線段DO的長為|DP﹣AP|的最大值.根據D,O兩點求出直線DO表達式為y=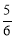 x, 又在直線 DO 上的點P的橫坐標為2,所以 p(2,
x, 又在直線 DO 上的點P的橫坐標為2,所以 p(2,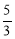 ),此時|DP﹣AP|=DO=
),此時|DP﹣AP|=DO=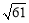 .
.
試題解析:【解析】
(1)∵由題意可得出:OA2+OB2=AB2,AO=4,BO=3,∴AB=5.∴圓的半徑為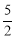 .
.
(2)證明:由題意可得出:M(2,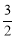 ).
).
∵C為劣弧AO的中點,由垂徑定理且 MC=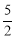 ,故 C(2,﹣1).
,故 C(2,﹣1).
如答圖1,過 D 作 DH⊥x 軸于 H,設 MC 與 x 軸交于 N,
則△ACN∽△ADH,
又∵DC=4AC,∴ DH=5NC=5,HA=5NA=10.∴D(﹣6,﹣5).
設直線BD表達式為:y=ax+b,
則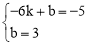 ,解得:
,解得: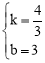 .∴直線BD表達式為:y=
.∴直線BD表達式為:y=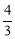 x+3.
x+3.
設 BD 與 x 軸交于Q,則Q(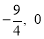 ).∴OQ=
).∴OQ=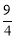 .∴
.∴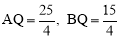 .
.
∵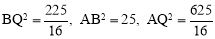 ,∴
,∴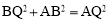 .∴△ABQ是直角三角形,即∠ABQ=90°.
.∴△ABQ是直角三角形,即∠ABQ=90°.
∴BD⊥AB,BD為⊙M的切線.
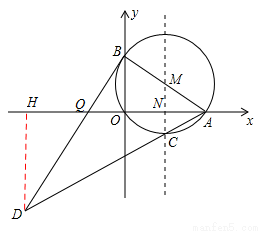
(3)如答圖2,取點A關于直線MC的對稱點O,連接DO并延長交直線MC于P,此P點為所求,且線段DO的長為|DP﹣AP|的最大值.
設直線DO表達式為 y=kx,
∴﹣5=﹣6k,解得:k=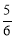 .
.
∴直線DO表達式為 y=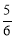 x
x
又∵在直線DO上的點P的橫坐標為2,∴y=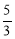 .∴P(2,
.∴P(2,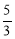 ).此時|DP﹣AP|=DO=
).此時|DP﹣AP|=DO=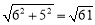 .
.
考點:1.圓的綜合題;2.勾股定理和逆定理;3.垂徑定理;4.相似三角形的判定和性質;5.待定系數法的應用;6.直線上點的坐標與方程的關系;7.切線的判定;8.軸對稱的應用(最短線路問題).


科目:初中數學 來源:2014-2015山東省威海市環翠區八年級上學期期中考試數學試卷(解析版) 題型:選擇題
在一次科技知識競賽中,兩組學生成績統計如下表,通過計算可知兩組的方差為 ,
, .下列說法:
.下列說法:
①兩組的平均數相同;
②甲組學生成績比乙組學生成績穩定;
③甲組成績的眾數>乙組成績的眾數;
④兩組成績的中位數均為80,但成績≥80的人數甲組比乙組多,從中位數來看,甲組成績總體比乙組好;⑤成績高于或等于90分的人數乙組比甲組多,高分段乙組成績比甲組好.
其中正確的共有( )
分數 | 50 | 60 | 70 | 80 | 90 | 100 | |
人數 | 甲組 | 2 | 5 | 10 | 13 | 14 | 6 |
乙組 | 4 | 4 | 16 | 2 | 12 | 12 | |
(A)2種 (B)3種 (C)4種 (D)5種
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣東卷)數學(解析版) 題型:選擇題
二次函數 的大致圖象如圖所示,關于該二次函數,下列說法錯誤的是( )
的大致圖象如圖所示,關于該二次函數,下列說法錯誤的是( )

A、函數有最小值
B、對稱軸是直線x=
C、當x< ,y隨x的增大而減小
,y隨x的增大而減小
D、當 -1 < x < 2時,y>0
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣東深圳卷)數學(解析版) 題型:選擇題
在﹣2,1,2,1,4,6中正確的是( )
A.平均數3 B.眾數是﹣2 C.中位數是1 D.極差為8
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣東卷)數學(解析版) 題型:解答題
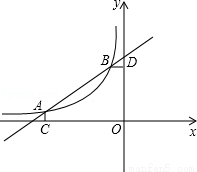
如圖,已知A ,B(-1,2)是一次函數
,B(-1,2)是一次函數 與反比例函數
與反比例函數
( )圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D。
)圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D。
(1)根據圖象直接回答:在第二象限內,當x取何值時,一次函數大于反比例函數的值?
(2)求一次函數解析式及m的值;
(3)P是線段AB上的一點,連接PC,PD,若△PCA和△PDB面積相等,求點P坐標。
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣東深圳卷)數學(解析版) 題型:選擇題
小明去爬山,在山腳看山頂角度為30°,小明在坡比為5:12的山坡上走1300米,此時小明看山頂的角度為60°,求山高( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣西欽州卷)數學(解析版) 題型:選擇題
如圖,等圓⊙O1和⊙O2相交于A、B兩點,⊙O1經過⊙O2的圓心O2,連接AO1并延長交⊙O1于點C,則∠ACO2的度數為( )

A.60° B.45° C.30° D.20°
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(浙江紹興卷)數學(解析版) 題型:解答題
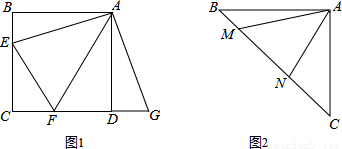
(1)如圖,正方形ABCD中,點E,F分別在邊BC,CD上,∠EAF=45°,延長CD到點G,使DG=BE,連結EF,AG.求證:EF=FG.
(2)如圖,等腰直角三角形ABC中,∠BAC=90°,AB=AC,點M,N在邊BC上,且∠MAN=45°,若BM=1,CN=3,求MN的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com