
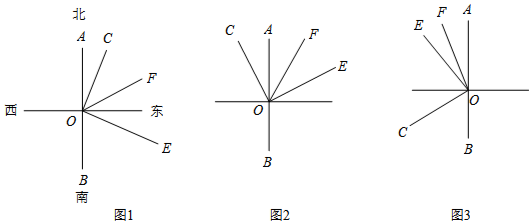
分析 (1)根據方向角的定義,以及∠COE=180-m-n,即可根據角的和差關系進行求解;
(2)根據∠COF=90°-∠EOF,∠EOF=$\frac{1}{2}$∠AOE=$\frac{1}{2}$(180°-∠DOE)=$\frac{1}{2}$∠BOE即可證得;
(3)根據角的和差,以及角平分線的定義即可求得∠BOE和∠COF之間的數量關系.
解答  解:(1)如圖1,∵2m+2n=180,
解:(1)如圖1,∵2m+2n=180,
∴m+n=90,
∵∠COE=180°-∠AOC-∠BOE=180°-m°-n°=90°;
∵射線OF平分∠AOE,
∴∠AOF=$\frac{1}{2}$(180°-∠BOE)=$\frac{1}{2}$(180°-n°),
∴∠COF=$\frac{1}{2}$(180°-n°)-m°,
由m+n=90可知,m=90-n,
∴∠COF=$\frac{1}{2}$(180°-n°)-m°=$\frac{1}{2}$(180°-n°)-90°+n°=$\frac{1}{2}$n°,
∴∠BOE=2∠COF.
故答案為:90,∠BOE=2∠COF;
(2)∠BOE和∠COF之間的數量關系不發生變化.
證明如下:如圖2,∵∠COE=90°
∴∠COF=90°-∠EOF
=90°-$\frac{1}{2}$∠AOE
=90°-$\frac{1}{2}$(180°-∠BOE)
=90°-90°+$\frac{1}{2}$∠BOE
=$\frac{1}{2}$∠BOE
∴∠BOE=2∠COF;
(3)∠BOE+2∠COF=360°.
理由:如圖3,∵∠COF=∠COE+∠EOF=90°+∠EOF,
∠BOE=∠COB+∠COE=90°+∠EOF,
∴∠BOE+∠COF=180°+2∠EOF,
又∵∠AOE=2∠EOF,
∴∠BOE+∠COF=180°+∠AOE,
∴∠BOE+2∠COF=360°.
點評 本題主要考查了方向角的定義,以及角平分線的定義的運用,對定義的熟練掌握是解題的關鍵.解題時注意角的和差關系的運用.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:解答題
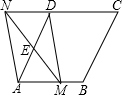 如圖,在菱形ABCD中,AB=20,∠DAB=60°,點E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MD,AN.
如圖,在菱形ABCD中,AB=20,∠DAB=60°,點E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MD,AN.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知AB=AC,BD=CD,E是AD上的一點,則下列結論中不成立的是( )
如圖,已知AB=AC,BD=CD,E是AD上的一點,則下列結論中不成立的是( )| A. | ∠BAD=∠CAD | B. | ∠BED=∠CED | C. | BE=CE | D. | AE=DE |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
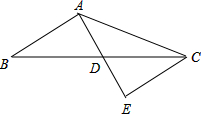 如圖,在△ABC中,AB=6,AC=10,AD是BC邊上的中線,且AD=4,延長AD到點E,使DE=AD,連接CE.
如圖,在△ABC中,AB=6,AC=10,AD是BC邊上的中線,且AD=4,延長AD到點E,使DE=AD,連接CE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
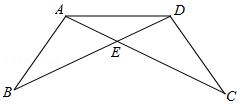 在一次數學課上,陳老師在黑板上畫出圖,并寫下了四個等式:
在一次數學課上,陳老師在黑板上畫出圖,并寫下了四個等式:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com