
分析 根據給定等式的變化即可找出變化規律“$\frac{1}{(n-1)n}$=$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2,且n為整數)”.
(1)依此規律代入數據即可求出結論;
(2)依此規律代入數據即可求出結論;
(3)利用類推法即可找出$\frac{1}{1×4}$=$\frac{1}{3}$×(1-$\frac{1}{4}$)、$\frac{1}{4×7}$=$\frac{1}{3}$×($\frac{1}{4}$-$\frac{1}{7}$)、$\frac{1}{7×11}$=$\frac{1}{3}$×($\frac{1}{7}$-$\frac{1}{11}$),將其代入$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×11}$中即可得出結論.
解答 解:觀察,發現:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,
∴$\frac{1}{(n-1)n}$=$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2,且n為整數).
(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
故答案為:$\frac{2016}{2017}$.
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{(n-1)n}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$=1-$\frac{1}{n}$=$\frac{n-1}{n}$.
(3)∵$\frac{1}{1×4}$=$\frac{1}{3}$×(1-$\frac{1}{4}$),$\frac{1}{4×7}$=$\frac{1}{3}$×($\frac{1}{4}$-$\frac{1}{7}$),$\frac{1}{7×11}$=$\frac{1}{3}$×($\frac{1}{7}$-$\frac{1}{11}$),
∴$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×11}$=$\frac{1}{3}$×[(1-$\frac{1}{4}$)+($\frac{1}{4}$-$\frac{1}{7}$)+($\frac{1}{7}$-$\frac{1}{11}$)]=$\frac{1}{3}$×(1-$\frac{1}{11}$)=$\frac{10}{33}$.
點評 本題考查了規律型中數字的變化類,根據等式中數的變化找出變化規律是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
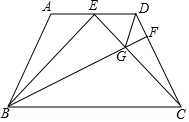 如圖,在四邊形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E為AD中點,連接BE,CE
如圖,在四邊形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E為AD中點,連接BE,CE查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com