
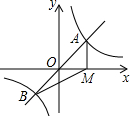
 如圖,函數y=kx(k≠0)與y=$\frac{3}{x}$的圖象交于A,B兩點,過點A作AM垂直于x軸,垂足為點M,則△BOM的面積為2.
如圖,函數y=kx(k≠0)與y=$\frac{3}{x}$的圖象交于A,B兩點,過點A作AM垂直于x軸,垂足為點M,則△BOM的面積為2. 分析 由函數y=kx(k≠0)與y=$\frac{4}{x}$的圖象交于A,B兩點,利用中心對稱的性質得到OA=OB,即MO為三角形ABM的中線,根據等底同高可得出三角形AOM與三角形BOM的面積相等,要求三角形BOM的面積即要求三角形AOM的面積,設A坐標為(a,b),可表示出OM與AM,利用三角形的面積公式表示出三角形AOM的面積,再將A的坐標代入反比例函數解析式中,得到ab的值,將ab的值代入表示出的面積中求出三角形AOM的面積,即為三角形BOM的面積.
解答 解:由題意得:OA=OB,則S△AOM=S△BOM,
設A(a,b)(a>0,b>0),故OM=a,AM=b,
將x=a,y=b代入反比例函數y=$\frac{4}{x}$得:b=$\frac{4}{a}$,即ab=4,
又∵AM⊥OM,即△AOM為直角三角形,
∴S△BOM=S△AOM=$\frac{1}{2}$OM•AM=$\frac{1}{2}$ab=2.
故答案是:2.
點評 此題考查了反比例函數解析式中k的幾何意義,其k的幾何意義為:過反比例函數y=$\frac{k}{x}$(k≠0)圖象上的點作兩坐標軸的垂線,兩垂線與兩坐標軸圍成矩形的面積等于|k|,熟練掌握此性質是解本題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 線段BD上有一點C,分別以BC、CD為邊作等邊△ABC和等邊△ECD,連接BE交AC于M,連接AD交CE于N,連接MN
線段BD上有一點C,分別以BC、CD為邊作等邊△ABC和等邊△ECD,連接BE交AC于M,連接AD交CE于N,連接MN查看答案和解析>>
科目:初中數學 來源: 題型:解答題
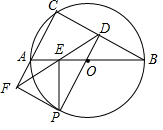 如圖,⊙O是△ABC的外接圓,AB是直徑,點D是弦BC的中點,延長DO交⊙O于點P,過點P作PE⊥AB于點E,作射線DE交CA的延長線于F點,連接PF.
如圖,⊙O是△ABC的外接圓,AB是直徑,點D是弦BC的中點,延長DO交⊙O于點P,過點P作PE⊥AB于點E,作射線DE交CA的延長線于F點,連接PF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com