實驗操作
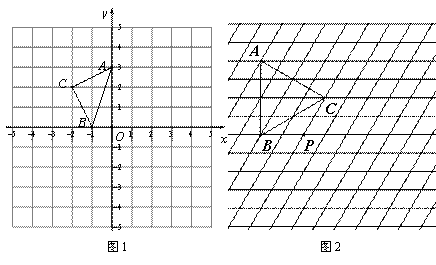
（1）如圖1，在平面直角坐標系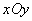
中，△
的頂點的橫、縱坐標都是整數，若將△以點
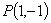為旋轉中心，按順時針方向旋轉
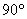得到△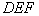
，請在坐標系中畫出點
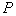及△；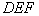
（2）如圖2，在菱形網格圖（最小的菱形的邊長為1，且有一個內角為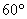
）中有一個等邊△，它的頂點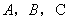
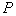都落在格點上，若將△以點為旋轉中心，按順時針方向旋轉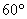得到△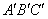
，請在菱形網格圖中畫出△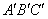.其中，點
旋轉到點
所經過的路線長為 .
 |
科目：初中數學 來源： 題型：
為了響應市政府“綠色出行”
的號召，小張上下班由自駕車方式改為騎自行車方式．已知小張單位與他家相距20千米，上下班高峰時段，自駕車的平均速度是自行平均車速度的2倍，騎自行車所用時間比自駕車所用時間多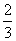
小時．求自駕車平均速度和自行車平均速度各是多少．
查看答案和解析>>
科目：初中數學 來源： 題型：
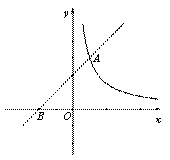
如圖，一次函數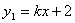
的圖象與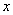
軸交于點
（
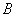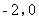），與函數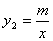
(
)的圖象交于點（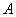
）．
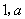（1）求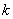
和
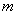的值；
（2）將函數（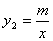
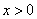）的圖象沿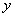
軸向下平移3個單位后交x軸于點
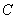．若點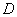
是平移后函數圖象上一點，且△
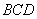的面積是3，直接寫出點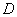的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
利用表格中的數據，可求出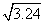
＋(4.123)2－
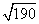的近似值是(結果保留整數)．
| A．3 | B．4 |
| C．5 | D．6 |
| a | a2 |
|
|
| 17 | 289 | 4.123 | 13.038 |
| 18 | 324 | 4.243 | 13.416 |
| 19 | 361 | 4.359 | 13.784 |
查看答案和解析>>
科目：初中數學 來源： 題型：
反比例函數y＝
(k為常數,k≠0)的圖象是雙曲線.當k＞0時，雙曲線兩個分支分別在
一、三象限,在每一個象限內,y隨x的增大而減小（簡稱增減性）；反比例函數的圖象關于
原點對稱（簡稱對稱性）．
這些我們熟悉的性質，可以通過說理得到嗎？
【嘗試說理】
我們首先對反比例函數y＝（k＞0）的增減性來進行說理．
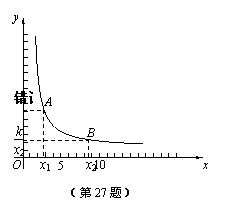
如圖，當x＞0時．
在函數圖象上任意取兩點A、B，設A(x1，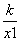
)，B(x2，
)，
且0＜x1＜ x2．
下面只需要比較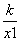和的大小．
—＝
．
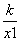∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
∴＜0．即
．
這說明：x1＜ x2時，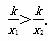
．也就是：自變量值增大了，對應的函數值反而變小了．
即：當x＞0時，y隨x的增大而減小．
同理，當x＜0時，y隨x的增大而減小．
（1）試說明：反比例函數y＝ （k＞0）的圖象關于原點對稱．
【運用推廣】
（2）分別寫出二次函數y＝ax2 (a＞0，a為常數)的對稱性和增減性，并進行說理．
對稱性： ；
增減性： ．
說理：
（3）對于二次函數y＝ax2＋bx＋c (a＞0，a，b，c為常數)，請你從增減性的角度，簡要解釋為何當x＝—
時函數取得最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
畫出△DEF… 
… 
B．
C． -5 D．5 
如圖，
，
與
相交于點
，
， 若
，則
等于_____．
中，AD∥BC，
，AB=AD=6，BC=9，以
為圓心在梯形內畫出一個最大的扇形（圖中陰影部分）的面積是 。