
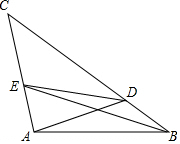
 △ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,則∠ADE=30°.
△ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,則∠ADE=30°. 分析 在BC上截BF=AB,利用全等三角形的判定和性質進行解答即可.
解答 解:在BC上截BF=AB,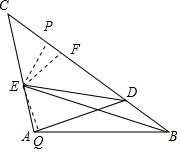
在△ABE與△FBE中
$\left\{\begin{array}{l}{∠ABE=∠FBE=20°}\\{BE=BE}\\{AB=BF}\end{array}\right.$,
∴△ABE≌△FBE(SAS),
∴∠BFE=∠BAE=100°,AE=EF,
∴∠EFP=∠EAD=80°,
過點E作EP⊥BC于點P,EQ⊥AD于點Q,
在Rt△PEF與Rt△QEA中$\left\{\begin{array}{l}{EF=AE}\\{∠EPF=∠EQA=90°}\\{∠PFE=∠EAQ}\end{array}\right.$,
∴Rt△PEF≌Rt△QEA,
∴PE=AE,
∴∠ADE=∠FDE═$\frac{1}{2}×60°=30°$,
故答案為:30°
點評 此題考查三角形內角和問題,關鍵是根據全等三角形的判定和性質進行解答.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
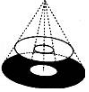 圓桌面(桌面中間有一個直徑為0.4m的圓洞)正上方的燈泡(看作一個點)發出的光線照射平行于地面的桌面后,在地面上形成如圖所示的圓環形陰影.已知桌面直徑為1.2m,桌面離地面1m,若燈泡離地面3m,則地面圓環形陰影的面積是( )
圓桌面(桌面中間有一個直徑為0.4m的圓洞)正上方的燈泡(看作一個點)發出的光線照射平行于地面的桌面后,在地面上形成如圖所示的圓環形陰影.已知桌面直徑為1.2m,桌面離地面1m,若燈泡離地面3m,則地面圓環形陰影的面積是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,點C在邊AD上,連接BD.
如圖,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,點C在邊AD上,連接BD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com