
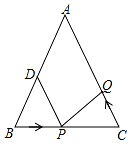
 如圖所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,點D為AB的中點.如果點P在線段BC上以1厘米/秒的速度由B點向C點運動,同時點Q在線段CA上由C點向A點運動.
如圖所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,點D為AB的中點.如果點P在線段BC上以1厘米/秒的速度由B點向C點運動,同時點Q在線段CA上由C點向A點運動.分析 (1)求出BP、CQ、CP,根據全等三角形的判定推出即可;
(2)設當點Q的運動速度為x厘米/時,時間是t小時,能夠使△BPD與△CQP全等,求出BD=5厘米,BP=t厘米,CP=(8-t)厘米,CQ=xt厘米,∠B=∠C,根據全等三角形的性質得出方程,求出方程的解即可.
解答 解:(1)全等,理由如下:
∵點P在線段BC上以1厘米/秒的速度由B點向C點運動,
∴BP=t厘米,
∵BC=8厘米,
∴CP=(8-t)厘米;
∵AB=AC=10厘米,點D為AB的中點,
∴∠B=∠C,BD=5厘米,
∵BP=CQ=t厘米=3厘米,
∴CP=8厘米-3厘米=5厘米=BD,
在△BPD和△CQP1中,$\left\{\begin{array}{l}{BD=CP}&{\;}\\{∠B=∠C}&{\;}\\{BP=CQ}&{\;}\end{array}\right.$,
∴△BPD≌△CQP(SAS);
(2)設當點Q的運動速度為x厘米/時,時間是t小時,能夠使△BPD與△CQP全等,
∵BD=5厘米,BP=t厘米,CP=(8-t)厘米,CQ=xt厘米,∠B=∠C,
∴當BP=CQ,BD=CP或BP=CP,BD=CQ時,△BPD與△CQP全等,
即①t=xt,5=8-t,
解得:x=1(不合題意,舍去),
②t=8-t,5=xt,
解得:x=4,
即當點Q的運動速度為4厘米/時,能夠使△BPD與△CQP全等.
點評 本題考查了全等三角形的判定和性質的應用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,用了分類討論思想.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
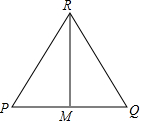 已知:如圖,△RPQ中,RP=RQ,M為PQ的中點.
已知:如圖,△RPQ中,RP=RQ,M為PQ的中點.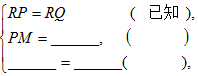
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
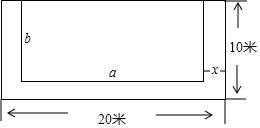 如圖,有一塊長為20米,寬10米的長方形土地,現將其余三面留出寬都是x米的小路,中間余下的長方形部分做菜地,用代數式表示:
如圖,有一塊長為20米,寬10米的長方形土地,現將其余三面留出寬都是x米的小路,中間余下的長方形部分做菜地,用代數式表示:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com