
如圖,點B、C、D都在半徑為6的⊙O上,過點C作AC∥BD交OB的延長線于點A,
連接CD,已知∠CDB=∠OBD=30°.
(1)求證:AC是⊙O的切線;
(2)求弦BD的長;
(3)求圖中陰影部分的面積.

(1)證明見解析;(2)6 ;(3)6π.
;(3)6π.
【解析】
試題分析:(1)連接OC,OC交BD于E,由∠CDB=∠OBD可知,CD∥AB,又AC∥BD,四邊形ABDC為平行四邊形,則∠A=∠D=30°,由圓周角定理可知∠COB=2∠D=60°,由內角和定理可求∠OCA=90°,證明切線..
(2)由(1)中的切線的性質和垂徑定理以及解直角三角形來求BD的長度.
(3)證明△OEB≌△CED,將陰影部分面積問題轉化為求扇形OBC的面積求解.
試題解析:【解析】
(1)證明:如答圖,連接OC,OC交BD于E,
∵∠CDB=30°,∴∠COB=2∠CDB=60°.
∵∠CDB=∠OBD,∴CD∥AB.
又∵AC∥BD,∴四邊形ABDC為平行四邊形.
∴∠A=∠D=30°.
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC.
又∵OC是⊙O的半徑,∴AC是⊙O的切線.

(2)由(1)知,OC⊥AC.
∵AC∥BD,∴OC⊥BD. ∴BE=DE.
∵在Rt△BEO中,∠OBD=30°,OB=6,∴BE=OBcos30°=3 .∴BD=2BE=6
.∴BD=2BE=6 .
.
(3)∵在△OEB和△CED中,∠OBE=∠CDE,∠OEB=∠CED,BE=DE,
∴△OEB≌△CED(AAS).∴S陰影=S扇形BOC.
∴S陰影= .
.
答:陰影部分的面積是6π.
考點:1.圓周角定理;2.平行的判定;3. 平行四邊形的判定和性質;4.三角形內角和定理;5.切線的判定和性質;6.垂徑定理;7. 特殊角的三角函數值;8.負整數指數冪;9.扇形面積的計算;10.轉換思想和數形結合思想的應用.


科目:初中數學 來源:2014年初中畢業升學考試(廣東深圳卷)數學(解析版) 題型:選擇題
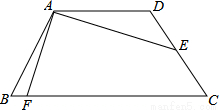
如圖,已知四邊形ABCD為等腰梯形,AD∥BC,AB=CD,AD= ,E為CD中點,連接AE,且AE=2
,E為CD中點,連接AE,且AE=2 ,∠DAE=30°,作AE⊥AF交BC于F,則BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,則BF=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣西欽州卷)數學(解析版) 題型:選擇題
如圖,正比例函數y=x與反比例函數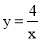 的圖象交于A(2,2)、B(﹣2,﹣2)兩點,當y=x的函數值大于
的圖象交于A(2,2)、B(﹣2,﹣2)兩點,當y=x的函數值大于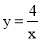 的函數值時,x的取值范圍是( )
的函數值時,x的取值范圍是( )

A.x>2 B.x<﹣2
C.﹣2<x<0或0<x<2 D.﹣2<x<0或x>2
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(浙江嘉興卷)數學(解析版) 題型:選擇題
2013年12月15日,我國“玉兔號”月球車順利抵達月球表面.月球離地球平均距離是384 400 000米,數據384 400 000用科學記數法表示為( )
A.3.844×108 B.3.844×107 C.3.844×106 D.38.44×106
查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(廣西欽州卷)數學(解析版) 題型:解答題
如圖,在正方形ABCD中,E、F分別是AB、BC上的點,且AE=BF.求證:CE=DF.

查看答案和解析>>
科目:初中數學 來源:2014年初中畢業升學考試(浙江嘉興卷)數學(解析版) 題型:填空題
如圖,在地面上的點A處測得樹頂B的仰角為α度,AC=7米,則樹高BC為 米(用含α的代數式表示).

查看答案和解析>>
科目:初中數學 來源:2014年滬教版初中數學七年級上冊第九章9.3整式的乘法練習卷(解析版) 題型:選擇題
計算(2a)3的結果是( )
A.6a B.8a C.2a3 D.8a3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com