
【題目】如圖,在![]() 中,
中,![]() (圓心
(圓心![]() 在
在![]() 內部)經過
內部)經過![]() 兩點,交線段
兩點,交線段![]() 于點
于點![]() 直徑
直徑![]() 交
交![]() 于點
于點![]() 點
點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 落在
落在![]() 上.連結
上.連結![]() .
.
![]() 求證:
求證:![]() .
.
![]() 在圓心
在圓心![]() 的運動過程中,
的運動過程中,
![]() 若
若![]() ,求
,求![]() 的長.
的長.
![]() 若點
若點![]() 關于
關于![]() 的對稱點落在
的對稱點落在![]() 邊上時,求
邊上時,求![]() 的值.(直接寫出答案)
的值.(直接寫出答案)
![]() 令
令![]() 與邊
與邊![]() 的另一個交點為
的另一個交點為![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() 若
若![]() ,垂足為點
,垂足為點![]() 求證:
求證:![]() .
.
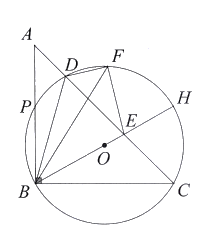
【答案】(1)證明見解析;(2)①![]() ;②
;②![]() 或
或![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)由對稱的性質可得∠A=∠BFD,結合∠BFD=∠C,即可推出結論;
(2)①先證∠DFE為直角,設![]() ,再用含a的代數式分別將FE,DE,EC表示出來,根據
,再用含a的代數式分別將FE,DE,EC表示出來,根據![]() 列方程即可求出CE的長;
列方程即可求出CE的長;
②分兩種情況討論,當點F關于AC的對稱點落在BF邊上時,連接DO,設FF'交AC于點M,證明BD=BE,△BOD是等腰直角三角形,即可求出結果;當點F關于AC的對稱點落在BE邊上時,點F'與點O重合,證明△DOF為等邊三角形,在Rt△DOE中,利用銳角三角函數即可求出結果;
(3)如圖作輔助線,先證明△QBG≌△ECM,推出BQ=CE,再證明DQ=DP=AD即可.
解:(1)![]() 點
點![]() 關于直線
關于直線![]() 對稱,
對稱,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①![]() 點
點![]() 關于直線
關于直線![]() 對稱,
對稱,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直徑,
是直徑,
![]() 由圓的軸對稱性可知:
由圓的軸對稱性可知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 設
設![]() ,則
,則![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ;
;
②如圖1,當點F關于AC的對稱點落在BF邊上時,連接DO,設FF'交AC于點M,則AC垂直平分FF',
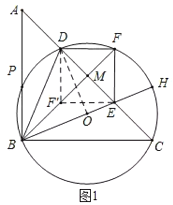
由(1)知,∠A=∠C=45°,∠ABC=90°,
∴BA=BC,∠ABM=∠CBM=45°,
∵點A,F關于直線BD對稱,
∴AD=DF,AB=FB,
又∵DB=DB,
∴△ABD≌△FBD(SSS),
∴∠ABD=∠FBD,
∵△BFE≌△BCE,
∴∠FBE=∠CBE,
∴∠ABD=∠FBD=∠FBE=∠CBE=22.5°,
∴∠DBE=∠DBF+∠EBF=45°,
∵OD=OB,
∴∠OBD=∠ODB=45°,
∴∠DOB=90°,
在△BDM與△BEM中,∠BDM=∠BEM=90°22.5°=67.5°,
∴BD=BE,
在等腰Rt△BOD中,設OB=OD=r,則BD=![]() ,
,
∴BE=![]() ,OE=
,OE=![]() ,
,
∴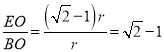 ;
;
如圖2,當點F關于AC的對稱點落在BE邊上時,
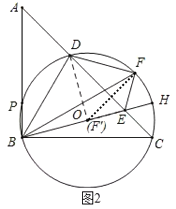
∵∠DF'E=∠DFE=90°,∠DOB=90°
∴點F'與點O重合,
連接OF,則OD=OF=DF,
∴△DOF為等邊三角形,
∴∠ODF=60°,
∴∠ODE=∠FDE=30°,
在Rt△DOE中,tan∠ODE=![]() =tan30°=
=tan30°=![]() ,
,
∴![]() ,
,
綜上所述,![]() 的值為
的值為![]() 或
或![]() ;
;
(3)連結![]() ;FC交
;FC交![]() 于點
于點![]() ,
,
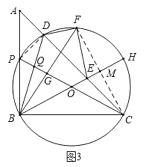
![]() ,
,
∴PC是直徑,
∵![]() ,
,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
∵![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某校為了了解初三年級600名學生的身體健康情況,從該年級隨機抽取了若干名學生,將他們按體重(均為整數,單位:![]() )分成五組(
)分成五組(![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ),并依據統計數據繪制了如下兩幅尚不完整的統計圖.
),并依據統計數據繪制了如下兩幅尚不完整的統計圖.
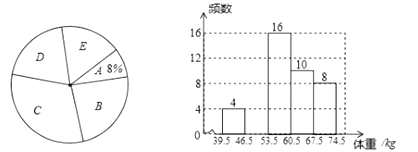
解答下列問題:
(1)這次抽樣調查的樣本容量是________,并補全頻數分布直方圖;
(2)![]() 組學生的頻率為_________,在扇形統計圖中
組學生的頻率為_________,在扇形統計圖中![]() 組的圓心角是__________度;
組的圓心角是__________度;
(3)請你估計該校初三年級體重超過![]() 的學生大約有多少名?
的學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形OABC的頂點A的坐標為(0,1),點B的坐標為(1,2),∠ABC=90°,連接AC.
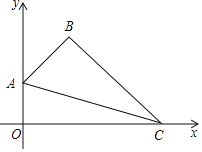
(1)求直線AC的函數表達式;
(2)點P是線段OC上一動點,從點O向點C運動,過點P作PM∥y軸,分別交AB或BC,AC于點M,N,其中點P的橫坐標為m,MN的長為n.
①當0<m≤1時,求n與m之間的函數關系式;
②當△AMN的面積最大時,請直接寫出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明在家鄉的樓頂上![]() 處測得池塘的一端
處測得池塘的一端![]() 處的俯角為
處的俯角為![]() ,測得池塘
,測得池塘![]() 處的俯角
處的俯角![]() ,
,![]() 、
、![]() 、
、![]() 三點在同一水平直線上.已知樓高
三點在同一水平直線上.已知樓高![]() 米,求池塘寬
米,求池塘寬![]() 為多少米?(參考數據:
為多少米?(參考數據:![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .結果保留一位小數.)
.結果保留一位小數.)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() )的圖象交于
)的圖象交于![]() ,
,![]() 兩點.
兩點.
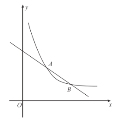
(1)求![]() 的值;
的值;
(2)求出一次函數與反比例函數的表達式;
(3)過點![]() 作
作![]() 軸的垂線,與直線
軸的垂線,與直線![]() 和函數
和函數![]() (
(![]() )的圖象的交點分別為點
)的圖象的交點分別為點![]() ,
,![]() ,當點
,當點![]() 在點
在點![]() 下方時,寫出
下方時,寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() (
(![]() ).
).
(1)求出二次函數圖象的對稱軸;
(2)若該二次函數的圖象經過點![]() ,且整數
,且整數![]() ,
,![]() 滿足
滿足![]() ,求二次函數的表達式;
,求二次函數的表達式;
(3)對于該二次函數圖象上的兩點![]() ,
,![]() ,設
,設![]() ,當
,當![]() 時,均有
時,均有![]() ,請結合圖象,直接寫出
,請結合圖象,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
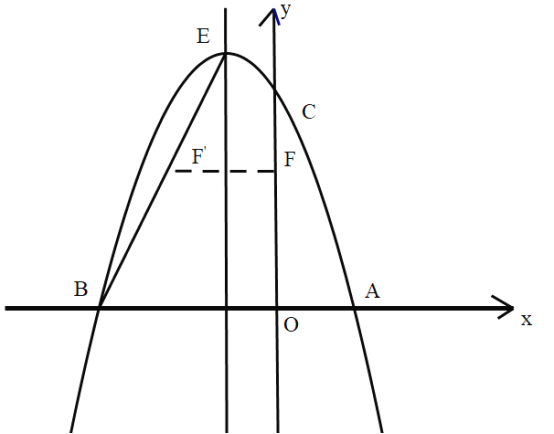
【題目】如圖,二次函數![]() 的圖像與
的圖像與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,直線l是拋物線的對稱軸,
,直線l是拋物線的對稱軸,![]() 是拋物線的頂點.
是拋物線的頂點.
(1)求拋物線的解析式及頂點![]() 的坐標;
的坐標;
(2)如圖,連接![]() ,線段
,線段![]() 上的點
上的點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 恰好在線段
恰好在線段![]() 上,求點
上,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
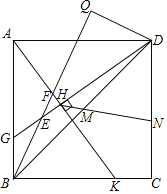
【題目】如圖,Q為正方形ABCD外一點,連接BQ,過點D作DQ⊥BQ,垂足為Q,G、K分別為AB、BC上的點,連接AK、DG,分別交BQ于F、E,AK⊥DG,垂足為點H,AF=5,DH=8,F為BQ中點,M為對角線BD的中點,連接HM并延長交正方形于點N,則HN的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com