
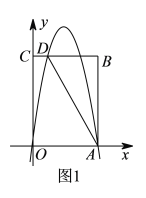
【題目】如圖,在平面直角坐標系中,四邊形OABC的頂點A的坐標為(0,1),點B的坐標為(1,2),∠ABC=90°,連接AC.
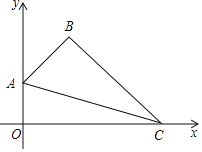
(1)求直線AC的函數表達式;
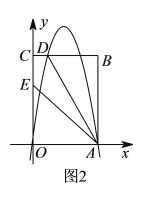
(2)點P是線段OC上一動點,從點O向點C運動,過點P作PM∥y軸,分別交AB或BC,AC于點M,N,其中點P的橫坐標為m,MN的長為n.
①當0<m≤1時,求n與m之間的函數關系式;
②當△AMN的面積最大時,請直接寫出m的值.
【答案】(1)y=﹣![]() x+1;(2)①n=
x+1;(2)①n=![]() m;②m=
m;②m=![]() 時,△AMN的面積最大為
時,△AMN的面積最大為![]()
【解析】
(1)先求出點C坐標,再利用待定系數法可求解析式;
(2)①先求出直線AB,BC的解析式,分別表示M,N兩點坐標,即可求解;
②分點M在AB上,點M在BC上兩種情況討論,利用一次函數的性質和二次函數的性質分別求出面積最大值,即可求解.
解:(1)如圖,過點B作BE⊥y軸于點E,作BF⊥OC于點F,連接OB,
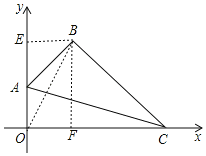
∵點A的坐標為(0,1),點B的坐標為(1,2),
∴OA=1,BE=OF=1,BF=OE=2,
∴AE=BE=1,
∴∠EAB=45°,
∴∠BAO=135°,
∵∠OAB+∠AOC+∠ABC+∠BCO=360°,
∴∠BCO=45°,
∴∠BCO=∠CBF=45°,
∴BF=CF=2,
∴OC=3,
∴點C(3,0),
設直線AC解析式為:y=kx+1,
∴0=3k+1,
∴k=﹣![]() ,
,
∴直線AC解析式為:y=﹣![]() x+1;
x+1;
(2)①如圖,∵A的坐標為(0,1),點B的坐標為(1,2),點C坐標(3,0)
易得直線AB解析式為:y=x+1,直線BC解析式為:y=﹣x+3,
當0<m≤1時,即點M在AB上,
∵點P的橫坐標為m,
∴點M(m,m+1),點N(m,﹣![]() m+1),
m+1),
∴MN=n=(m+1)﹣(﹣![]() m+1)=
m+1)=![]() m;
m;
②當0<m≤1時,MN=n=![]() m,
m,
∴S△AMN=![]() ×m×
×m×![]() m=
m=![]() m2,
m2,
∴當m=1時,△AMN的面積最大為![]() ,
,
當1<m≤3時,同①可得:M'N'=n=﹣m+3﹣(﹣![]() m+1)=﹣
m+1)=﹣![]() m+2,
m+2,
∴S△AMN=![]() ×m×(﹣
×m×(﹣![]() m+2)=﹣
m+2)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴當m=![]() 時,△AMN的面積最大為
時,△AMN的面積最大為![]() ,
,
綜上所述:當m=![]() 時,△AMN的面積最大為
時,△AMN的面積最大為![]() .
.



科目:初中數學 來源: 題型:
【題目】房山某中學改革學生的學習模式,變“老師要學生學習”為“學生自主學習”,培養了學生自主學習的能力.小華與小明同學就“最喜歡哪種學習方式”隨機調查了他們周圍的一些同學,根據收集到的數據繪制了以下的兩個統計圖.請根據下面兩個不完整的統計圖回答以下問題:

(1)這次抽樣調查中,共調查了 名學生;
(2)補全兩幅統計圖;
(3)根據抽樣調查的結果,估算該校1000名學生中大約有多少人選擇“小組合作學習”?
查看答案和解析>>
科目:初中數學 來源: 題型:
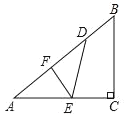
【題目】如圖,已知一個三角形紙片![]() ,其中
,其中![]() ,
,![]() 分別是
分別是![]() 邊上的點,連接
邊上的點,連接![]() .
.
(1)如圖,若將紙片![]() 的一角沿
的一角沿![]() 折疊,折疊后點
折疊,折疊后點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,且使S四邊形ECBF
處,且使S四邊形ECBF![]() ,求
,求![]() 的長;
的長;
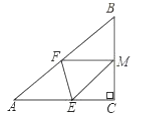
(2)如圖,若將紙片![]() 的一角沿
的一角沿![]() 折疊,折疊后點
折疊,折疊后點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,且使
處,且使![]() .試判斷四邊形
.試判斷四邊形![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,矩形OABC的頂點A,C的坐標分別為(4,0),(0,6),直線AD交BC于點D.tan∠OAD=2,拋物線
,矩形OABC的頂點A,C的坐標分別為(4,0),(0,6),直線AD交BC于點D.tan∠OAD=2,拋物線![]() 過A,D兩點.
過A,D兩點.
(![]() )求點D的坐標和拋物線M1的表達式.
)求點D的坐標和拋物線M1的表達式.
(![]() )點P是拋物線M1對稱軸上一動點,當∠CPA=90°時,求所有滿足條件的點P的坐標.
)點P是拋物線M1對稱軸上一動點,當∠CPA=90°時,求所有滿足條件的點P的坐標.
(![]() )如圖
)如圖![]() ,點E(0,4),連接AE,將拋物線M1的圖象向下平移m(m>0)個單位得到拋物線M2.
,點E(0,4),連接AE,將拋物線M1的圖象向下平移m(m>0)個單位得到拋物線M2.
①設點D平移后的對應點為點D',當點D'恰好落在直線AE上時,求m的值.
②當![]() 時,若拋物線M2與直線AE有兩個交點,求m的取值范圍.
時,若拋物線M2與直線AE有兩個交點,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
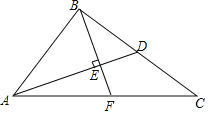
【題目】如圖,在Rt△ACB中,∠ABC=90°,D為BC邊的中點,BE⊥AD于點E,交AC于F,若AB=4,BC=6,則線段EF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】心理學家研究發現,一般情況下,一節課40分鐘中,學生的注意力隨教師講課的變化而變化,開始上課時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指標數y隨時間x(分鐘)的變化規律如圖所示(其中AB、BC分別為線段,CD為雙曲線的一部分):
(1)開始上課后第五分鐘時與第三十分鐘時相比較,何時學生的注意力更集中?
(2)一道數學競賽題,需要講16分鐘,為了效果較好,要求學生的注意力指標數最低達到36,那么經過適當安排,老師能否在學生注意力達到所需的狀態下講解完這道題目?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是![]() 的一定點,D是弦AB上的一定點,P是弦CB上的一動點.連接DP,將線段PD繞點P順時針旋轉
的一定點,D是弦AB上的一定點,P是弦CB上的一動點.連接DP,將線段PD繞點P順時針旋轉![]() 得到線段
得到線段![]() .射線
.射線![]() 與
與![]() 交于點Q.已知
交于點Q.已知![]() ,設P,C兩點間的距離為xcm,P,D兩點間的距離
,設P,C兩點間的距離為xcm,P,D兩點間的距離![]() ,P,Q兩點的距離為
,P,Q兩點的距離為![]() .
.
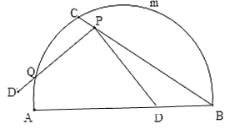
小石根據學習函數的經驗,分別對函數![]() ,
,![]() ,隨自變量x的變化而變化的規律進行了探究,下面是小石的探究過程,請補充完整:
,隨自變量x的變化而變化的規律進行了探究,下面是小石的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,分別得到了![]() ,
,![]() ,與x的幾組對應值:
,與x的幾組對應值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐標系xOy中,描出補全后的表中各組數據所對應的點![]() ,
,![]() ,并畫出函數
,并畫出函數![]() ,
,![]() 的圖象;
的圖象;
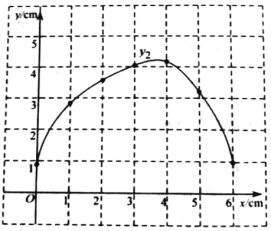
(3)結合函數圖象,解決問題:連接DQ,當△DPQ為等腰三角形時,PC的長度約為_____cm.(結果保留一位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
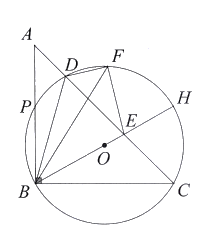
【題目】如圖,在![]() 中,
中,![]() (圓心
(圓心![]() 在
在![]() 內部)經過
內部)經過![]() 兩點,交線段
兩點,交線段![]() 于點
于點![]() 直徑
直徑![]() 交
交![]() 于點
于點![]() 點
點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 落在
落在![]() 上.連結
上.連結![]() .
.
![]() 求證:
求證:![]() .
.
![]() 在圓心
在圓心![]() 的運動過程中,
的運動過程中,
![]() 若
若![]() ,求
,求![]() 的長.
的長.
![]() 若點
若點![]() 關于
關于![]() 的對稱點落在
的對稱點落在![]() 邊上時,求
邊上時,求![]() 的值.(直接寫出答案)
的值.(直接寫出答案)
![]() 令
令![]() 與邊
與邊![]() 的另一個交點為
的另一個交點為![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() 若
若![]() ,垂足為點
,垂足為點![]() 求證:
求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某體育老師隨機抽取了九年級甲、乙兩班部分學生進行一分鐘跳繩的測試,并對成績進行統計分析,繪制了頻數分布表和統計圖,請你根據圖表中的信息完成下列問題:
分組 | 頻數 | 頻率 |
第一組(0≤x<120) | 3 | 0.15 |
第二組(120≤x<160) | 8 | a |
第三組(160≤x<200) | 7 | 0.35 |
第四組(200≤x<240) | b | 0.1 |
(1)頻數分布表中a=____,b=_____,并將統計圖補充完整;
(2)如果該校九年級共有學生360人,估計跳繩能夠一分鐘完成160或160次以上的學生有多少人?
(3)已知第一組中有兩個甲班學生,第四組中只有一個甲班學生,老師隨機從這兩個組中各選一名學生談測試體會,則所選兩人正好都是甲班學生的概率是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com