
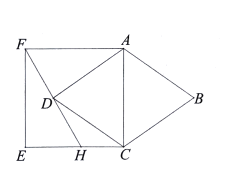
【題目】如圖,以菱形![]() 的對角線
的對角線![]() 為邊,在
為邊,在![]() 的左側作正方形
的左側作正方形![]() 連結
連結![]() 并延長交
并延長交![]() 于點
于點![]() .若正方形
.若正方形![]() 的面積是菱形
的面積是菱形![]() 面積的
面積的![]() 倍,
倍,![]() ,則
,則![]() _________________.
_________________.
【答案】![]()
【解析】
連接BD交AC于G,由菱形性質可得AC與BD互相垂直平分,菱形面積等于AC與BD的積的一半,可得S菱形ABCD=ACDG,因為G是AC中點且DG∥EC∥AF,根據平行線分線段成比例定理可知點D也是FH中點,故DG是梯形ACHF中位線,DG=![]() (CH+AF)=
(CH+AF)=![]() (CH+EF),因此菱形ABCD面積可用含EF的式子表示,然后以正方形面積為菱形面積的1.4倍為等量關系列方程,即可求出EF的長.
(CH+EF),因此菱形ABCD面積可用含EF的式子表示,然后以正方形面積為菱形面積的1.4倍為等量關系列方程,即可求出EF的長.
解:連接BD,交AC于點G,
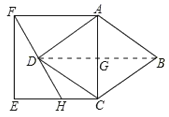
∵四邊形ABCD是菱形,
∴AC⊥BD,DB=2DG,AG=CG,
∴S菱形ABCD=![]() ACDB=ACDG,
ACDB=ACDG,
∵四邊形ACEF是正方形,
∴EF=AF=AC=CE,AF∥EC,AC⊥EC,
∴DB∥CE∥AF,
∴![]() ,即DG為梯形ACHF的中位線,
,即DG為梯形ACHF的中位線,
∴DG=![]() (CH+AF)=
(CH+AF)=![]() (CH+EF),
(CH+EF),
∵CH=6,正方形![]() 的面積是菱形
的面積是菱形![]() 面積的
面積的![]() 倍,
倍,
∴EF2=1.4ACDG,
∴EF2=1.4EF·![]() (6+EF),
(6+EF),
∴EF=14,
故答案為:14.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
【題目】某校積極開展“陽光體育”活動,并開設了跳繩、足球、籃球、跑步四種運動項目,為了解學生最喜愛哪一種項目,隨機抽取了部分學生進行調查,并繪制了如下的條形統計圖和扇形統計圖(部分信息未給出).
(1)求本次被調查的學生人數;
(2)補全條形統計圖;
(3)該校共有3000名學生,請估計全校最喜愛籃球的人數比最喜愛足球的人數多多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
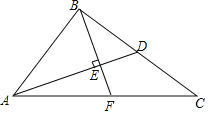
【題目】如圖,在Rt△ACB中,∠ABC=90°,D為BC邊的中點,BE⊥AD于點E,交AC于F,若AB=4,BC=6,則線段EF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
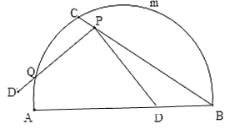
【題目】如圖,C是![]() 的一定點,D是弦AB上的一定點,P是弦CB上的一動點.連接DP,將線段PD繞點P順時針旋轉
的一定點,D是弦AB上的一定點,P是弦CB上的一動點.連接DP,將線段PD繞點P順時針旋轉![]() 得到線段
得到線段![]() .射線
.射線![]() 與
與![]() 交于點Q.已知
交于點Q.已知![]() ,設P,C兩點間的距離為xcm,P,D兩點間的距離
,設P,C兩點間的距離為xcm,P,D兩點間的距離![]() ,P,Q兩點的距離為
,P,Q兩點的距離為![]() .
.
小石根據學習函數的經驗,分別對函數![]() ,
,![]() ,隨自變量x的變化而變化的規律進行了探究,下面是小石的探究過程,請補充完整:
,隨自變量x的變化而變化的規律進行了探究,下面是小石的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,分別得到了![]() ,
,![]() ,與x的幾組對應值:
,與x的幾組對應值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐標系xOy中,描出補全后的表中各組數據所對應的點![]() ,
,![]() ,并畫出函數
,并畫出函數![]() ,
,![]() 的圖象;
的圖象;
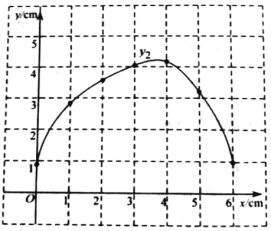
(3)結合函數圖象,解決問題:連接DQ,當△DPQ為等腰三角形時,PC的長度約為_____cm.(結果保留一位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() (圓心
(圓心![]() 在
在![]() 內部)經過
內部)經過![]() 兩點,交線段
兩點,交線段![]() 于點
于點![]() 直徑
直徑![]() 交
交![]() 于點
于點![]() 點
點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 落在
落在![]() 上.連結
上.連結![]() .
.
![]() 求證:
求證:![]() .
.
![]() 在圓心
在圓心![]() 的運動過程中,
的運動過程中,
![]() 若
若![]() ,求
,求![]() 的長.
的長.
![]() 若點
若點![]() 關于
關于![]() 的對稱點落在
的對稱點落在![]() 邊上時,求
邊上時,求![]() 的值.(直接寫出答案)
的值.(直接寫出答案)
![]() 令
令![]() 與邊
與邊![]() 的另一個交點為
的另一個交點為![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() 若
若![]() ,垂足為點
,垂足為點![]() 求證:
求證:![]() .
.
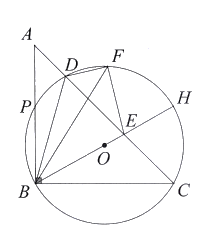
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC與△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.

提出問題:如圖1,當∠ADB=∠ACB=90°時,求證:AD=BC;
類比探究:如圖2,當∠ADB≠∠ACB時,AD=BC是否還成立?并說明理由.
綜合運用:如圖3,當β=18°,BC=1,且AB⊥BC時,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月23日為世界閱讀日,為響應黨中央“倡導全民閱讀,建設書香會”的號召,某校團委組織了一次全校學生參加的“讀書活動”大賽為了解本次賽的成績,校團委隨機抽取了部分學生的成績(成績![]() 取整數,總分100分)作為本進行統計,制成如下不完整的統計圖表(頻數頻率分布表和頻數分布直方圖):
取整數,總分100分)作為本進行統計,制成如下不完整的統計圖表(頻數頻率分布表和頻數分布直方圖):
成績 | 頻數(人) | 頻率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
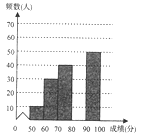
根據所給信息,解答下列問題:
(1)抽取的樣本容量是 ;![]() ,
,![]() ;
;
(2)補全頻數分布直方圖;這200名學生成績的中位數會落在 分數段;
(3)全校有1200名學生參加比賽,若得分為90分及以上為優秀,請你估計全校參加比賽成績優秀的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了測量休閑涼亭AB的高度,某數學興趣小組在水平地面D處豎直放置一個標桿CD,并在地面上水平放置一個平面鏡E,使得B、E、D在同一水平線上,如圖所示.該小組在標桿的F處通過平面鏡E恰好觀測到涼亭頂端A,在F處測得涼亭A頂端的仰角為30°,平面鏡E的俯角為45°,FD=2米,求休閑涼亭AB的高度.(結果保留根號)
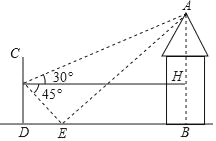
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com