
【題目】如圖,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(請填空)
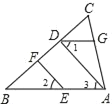
解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
【答案】∠3,兩直線平行,同位角相等,等量代換,DG,內錯角相等,兩直線平行,∠DGA,兩直線平行,同旁內角互補,已知,110°,等式的性質.
【解析】
根據平行線的性質和已知求出∠1=∠3,根據平行線的判定定理推出AB∥DG;接下來,再根據平行線的性質得出∠BAC+∠DGA=180°,進而不難求得∠AGD的度數.
解:∵EF∥AD,
∴∠2=∠3(兩直線平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代換),
∴AB∥DG(內錯角相等,兩直線平行),
∴∠BAC+∠DGA=180°(兩直線平行,同旁內角互補),
∵∠BAC=70°(已知),
∴∠AGD=110°(等式的性質).
故答案為:∠3,兩直線平行,同位角相等,等量代換,DG,內錯角相等,兩直線平行,∠DGA,兩直線平行,同旁內角互補,已知,110°,等式的性質.


科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有紅、黃、白三種顏色球共100個,它們除顏色外都相同,其中黃球個數是白球個數的2倍少5個.已知從袋中摸出一個球是紅球的概率是![]() .
.
(1)求袋中紅球的個數;
(2)求從袋中摸出一個球是白球的概率;
(3)取走10個球(其中沒有紅球)后,求從剩余的球中摸出一個球是紅球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點0是AC邊上一動點,過點0作DE,使DE∥BC,DE交∠ACB的角平分線于點D,交∠ACB的外角平分線于點E.
(1)求證:OD=OE;
(2)當點0運動到何處時,四邊形CDAE是矩形?請證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角形角平分線交點或三角形內切圓的圓心都稱為三角形的內心.按此說法,四邊形的四個角平分線交于一點,我們也稱為“四邊形的內心”.
(1)試舉出一個有內心的四邊形.
(2)探究:對于任意四邊形ABCD,如果有內心,則四邊形的邊長具備何種條件?為什么?
(3)探究:腰長為![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的內心,若沿圖中虛線剪開,O仍然是四邊形ABDE的內心,此時裁剪線有多少條?
的等腰直角三角形ABC,∠C=90°,O是△ABC的內心,若沿圖中虛線剪開,O仍然是四邊形ABDE的內心,此時裁剪線有多少條?
(4)問題(3)中,O是四邊形ABDE內心,且四邊形ABDE是等腰梯形,求DE的長?
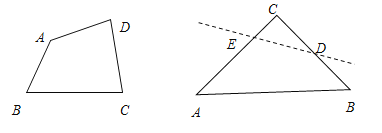
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是ABCD的邊CD的中點,延長AE交BC的延長線于點F.
(1)求證:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△AOB是直角三角形,∠AOB=90°,邊AB與y軸交于點C.

(1)若∠A=∠AOC,試說明:∠B=∠BOC;
(2)延長AB交x軸于點E,過O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度數;
(3)如圖,OF平分∠AOM,∠BCO的平分線交FO的延長線于點P,∠A=40°,當△ABO繞O點旋轉時(邊AB與y軸正半軸始終相交于點C),問∠P的度數是否發生改變?若不變,求其度數;若改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在黃州服裝批發市場,某種品牌的時裝當季節將來臨時,價格呈上升趨勢,設這種時裝開始時定價為20元,并且每周(7天)漲價2元,從第6周開始保持30元的價格平穩銷售;從第12周開始,當季節即將過去時,平均每周減價2元,直到第16周周末,該服裝不再銷售.
(1)試建立銷售價y與周次x之間的函數關系式;
(2)若這種時裝每件進價Z與周次x次之間的關系為Z=﹣0.125(x﹣8)2+12,1≤x≤16,且x為整數,試問該服裝第幾周出售時,每件銷售利潤最大?最大利潤為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A、B、C是數軸上的三點,點C表示的數是6,點B與點C之間的距離是4,點B與點A的距離是12,點P為數軸上一動點.
(1)數軸上點A表示的數為 .點B表示的數為 ;
(2)數軸上是否存在一點P,使點P到點A、點B的距離和為16,若存在,請求出此時點P所表示的數;若不存在,請說明理由;
(3)點P以每秒1個單位長度的速度從C點向左運動,點Q以每秒2個單位長度從點B出發向左運動,點R從點A以每秒5個單位長度的速度向右運動,它們同時出發,運動的時間為t秒,請求點P與點Q,點R的距離相等時t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,有一個等腰直角三角形AOB,∠OAB=90°,直角邊AO在x軸上,且AO=1.將Rt△AOB繞原點O順時針旋轉90°得到等腰直角三角形A1OB1,且A1O=2AO,再將Rt△A1OB1繞原點O順時針旋轉90°得到等腰三角形A2OB2,且A2O=2A1O……依此規律,得到等腰直角三角形A2 017OB2 017.則點B2 017的坐標( )

A. (22 017,-22 017) B. (22 016,-22 016) C. (22 017,22 017) D. (22 016,22 016)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com