
【題目】如圖,已知A、B、C是數軸上的三點,點C表示的數是6,點B與點C之間的距離是4,點B與點A的距離是12,點P為數軸上一動點.
(1)數軸上點A表示的數為 .點B表示的數為 ;
(2)數軸上是否存在一點P,使點P到點A、點B的距離和為16,若存在,請求出此時點P所表示的數;若不存在,請說明理由;
(3)點P以每秒1個單位長度的速度從C點向左運動,點Q以每秒2個單位長度從點B出發向左運動,點R從點A以每秒5個單位長度的速度向右運動,它們同時出發,運動的時間為t秒,請求點P與點Q,點R的距離相等時t的值.

【答案】(1)-10;2 (2)存在;﹣12或4 (3)![]() 或4
或4
【解析】
(1)結合數軸可知點A和點B都在點C的左邊,且點A小于0,在根據題意列式計算即可得到答案;
(2)因為AB=12,則P不可能在線段AB上,所以分兩種情況:
①當點P在BA的延長線上時,②當點P在AB的延長線上時,進行討論,即可得到答案;
(3)根據題意“t秒P點到點Q,點R的距離相等”,則此時點P、Q、R所表示的數分別是6﹣t,2﹣2t,﹣10+5t,分①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t)兩種情況,計算即可得到答案.
解:(1)由題意可知點A和點B都在點C的左邊,且點A小于0,則由題意可得數軸上點B表示的數為6-4=2,點A表示的數為2-10=﹣10,故答案為:﹣10,2;
(2)∵AB=12,
∴P不可能在線段AB上,
所以分兩種情況:
①如圖1,當點P在BA的延長線上時,PA+PB=16,

∴PA+PA+AB=16,
2PA=16﹣12=4,
PA=2,
則點P表示的數為﹣12;
②如圖2,當點P在AB的延長線上時,同理得PB=2,

則點P表示的數為4;
綜上,點P表示的數為﹣12或4;
(3)由題意得:t秒P點到點Q,點R的距離相等,則此時點P、Q、R所表示的數分別是6﹣t,2﹣2t,﹣10+5t,
①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),解得t=![]() ;
;
②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t),解得t=4;
答:點P與點Q,點R的距離相等時t的值是![]() 或4秒.
或4秒.


科目:初中數學 來源: 題型:
【題目】計算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(請填空)
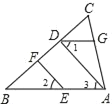
解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 一個游戲中獎的概率是![]() ,則做100次這樣的游戲一定會中獎
,則做100次這樣的游戲一定會中獎
B. 為了了解全國中學生的心理健康狀況,應采用普查的方式
C. 一組數據0,1,2,1,1的眾數和中位數都是1
D. 若甲組數據的方差![]() ,乙組數據的方差
,乙組數據的方差![]() ,則乙組數據比甲組數據穩定
,則乙組數據比甲組數據穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,點C在⊙O 上,點P是直徑AB上的一點,(不與A,B重合),過點P作AB的垂線交BC的延長線于點Q.
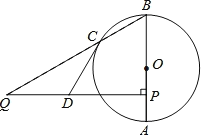
(1)點D在線段PQ上,且DQ=DC.求證:CD是⊙O的切線;
(2)若sin∠Q=![]() ,BP=6,AP=2,求QC的長.
,BP=6,AP=2,求QC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著我國經濟的高速發展,有著“經濟晴雨表”之稱的股市也得到迅速的發展,下表是今年上證指數某一周星期一至星期五的變化情況.(注:上周五收盤時上證指數為2019點,每一天收盤時指數與前一天相比,漲記為“![]() ”,跌記為“
”,跌記為“![]() ”
” ![]()
星期 | 一 | 二 | 三 | 四 | 五 |
指數的變化(與前一天比較) |
|
|
|
|
|
(1)本周星期二收盤時的上證指數是 點;
(2)本周星期五收盤時的上證指數與上周星期五收盤時的上證指數相比,是增加了還是減少了?
(3)本周哪一天收盤時的上證指數最高?哪一天收盤時的上證指數最低?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每一個小正方形的邊長為1.△ABC的三個頂點都在格點上,A、C的坐標分別是(﹣4,6),(﹣1,4).
(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出△ABC向右平移6個單位的△A1B1C1,并寫出C1的坐標 ;
(3)請畫出△ABC關于原點O對稱的△A2B2C2 , 并寫出點C2的坐標 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個點從數軸上的原點開始,先向左移動2cm到達A點,再向左移動3cm到達B點,然后向右移動9cm到達C點。
![]()
(1)用1個單位長度表示1cm,請你在數軸上表示出A. B. C三點的位置;
(2)把點C到點A的距離記為CA,則CA=______cm.
(3)若點B以每秒2cm的速度向左移動,同時A. C點分別以每秒1cm、4cm的速度向右移動。設移動時間為t秒,試探索:CAAB的值是否會隨著t的變化而改變?請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某校組織的初中數學應用能力競賽中,每班參加比賽的人數相同,成績分為A、B、C、D四個等級,其中相應等級的得分依次記為100分、90分、80分、70分,學校將八年級的一班和二班的成績整理并繪制成如下的統計圖,二班D級共有4人.

請你根據以上提供的信息解答下列問題:
(1)求此競賽中一班共有多少人參加比賽,并補全條形統計圖.
(2)扇形統計圖中A級對應的圓心角度數是 .
(3)此次競賽中二班在C級以上(包括C級)的人數為 .
(4)請你將表格補充完成:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com