Question

20．如圖，在梯形ABCD中，AD∥BC，AC與BD相交于點O，AC=BC，點E在DC的延長線上，∠BEC=∠ACB，已知BC=9，cos∠ABC=$\frac{1}{3}$．
（1）求證：BC²=CD•BE；
（2）設AD=x，CE=y，求y與x之間的函數解析式，并寫出定義域；
（3）如果△DBC∽△DEB，求CE的長．

Answer 1

分析 （1）只要證明△DAC∽△CEB，得到$\frac{DC}{CB}$=$\frac{AC}{BE}$，再根據題意AC=BC，即可證明．
（2）過點C作CF⊥AB于F，AG⊥BC于G，DH⊥BC于H．由△CEB∽△DAC，得$\frac{CE}{AD}$=$\frac{BC}{CD}$，由此即可解決問題．
（3）首先證明四邊形ABCD是等腰梯形，再證明△ABG≌△DCH，推出CH=BG=2，推出x=GH=BC-BG-CH=9-2-2=5，再利用（2）中即可即可解決問題．

解答 解：（1）∵∠DCB=∠ACD+∠ACB，∠DCB=∠EBC+∠BEC，∠ACB=∠BEC，
∴∠ACD=∠EBC，
∵AD∥BC，
∴∠DAC=∠ACB=∠CEB，
∴△DAC∽△CEB，
∴$\frac{DC}{CB}$=$\frac{AC}{BE}$，
∴BC•AC=CD•BE，
∵AC=BC，
∴BC²=CD•BE．

（2）過點C作CF⊥AB于F，AG⊥BC于G，DH⊥BC于H．
在Rt△CBF中，BF=BC•cos∠ABC=9×$\frac{1}{3}$=3，
∴AB=6，
在Rt△ABG中，BG=AB•cos∠ABC=6×$\frac{1}{3}$=2，
∵AD∥BC，DH=AG，
∴DH²=AG²=AB²-BG²=6²-2²=32，
∵AG∥DH，
∴GH=AD=x，
∴CH=BC-BG-GH=7-x，
∴CD=$\sqrt{C{H}^{2}+D{H}^{2}}$=$\sqrt{（7-x）^{2}+32}$=$\sqrt{{x}^{2}-14x+81}$，
∵△CEB∽△DAC，
∴$\frac{CE}{AD}$=$\frac{BC}{CD}$，
∴$\frac{y}{x}$=$\frac{9}{\sqrt{{x}^{2}-14x+81}}$，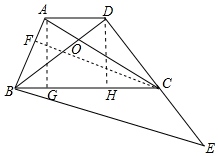
∴y=$\frac{9x}{\sqrt{{x}^{2}-14x+81}}$，
∴y=$\frac{9x\sqrt{{x}^{2}-14x+81}}{{x}^{2}-14x+81}$（x＞0且x≠9）．

（3）∵△DBC∽△DEB，∠CDB=∠BDE，∠CBD＜∠DBC，
∴∠DBC=∠DEB=∠ACB，
∴OB=OC，
∵AD∥BC，
∴$\frac{AC}{OC}$=$\frac{BD}{OB}$，
∴AC=BD，
∴四邊形ABCD是等腰梯形，
∴AB=CD，∠ABC=∠DCB，
∵∠AGB=∠DHC=90°，
∴△ABG≌△DCH，
∴CH=BG=2，
∴x=GH=BC-BG-CH=9-2-2=5．
∴CE=y=$\frac{15}{2}$．

點評 本題考查相似三角形綜合題、銳角三角函數、勾股定理、等腰梯形的判定和性質等知識，解題的關鍵是靈活運用所學知識解決問題，學會添加常用輔助線，屬于中考壓軸題．