
分析 可令x5+$\frac{1}{{x}^{5}}$=m,則x10+x5+$\frac{1}{{x}^{5}}$+$\frac{1}{{x}^{10}}$=15250變形為(x5+$\frac{1}{{x}^{5}}$)2+(x5+$\frac{1}{{x}^{5}}$)-15252=0,得到m2+m-15252=0,解得m,再令x+$\frac{1}{x}$=a,得到x5+$\frac{1}{{x}^{5}}$=(x4+$\frac{1}{{x}^{4}}$)(x+$\frac{1}{x}$)-(x3+$\frac{1}{{x}^{3}}$)=a(a4-4a2+2)-(a3-3a)=a5-5a3+5a,得到a5-5a3+5a=123,再根據(jù)公因式法解方程即可求解.
解答 解:令x5+$\frac{1}{{x}^{5}}$=m,
則x10+x5+$\frac{1}{{x}^{5}}$+$\frac{1}{{x}^{10}}$=15250變形為(x10+$\frac{1}{{x}^{10}}$)+(x5+$\frac{1}{{x}^{5}}$)-15250=0,
(x5+$\frac{1}{{x}^{5}}$)2+(x5+$\frac{1}{{x}^{5}}$)-15252=0,
即m2+m-15252=0,
(m-123)(m+124)=0,
解得m1=123,m2=-124,
∵x為正數(shù),
∴m2=-124不合題意舍去,
∴m=123,
令x+$\frac{1}{x}$=a,
則x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=a2-2,
x3+$\frac{1}{{x}^{3}}$=(x2+$\frac{1}{{x}^{2}}$)(x+$\frac{1}{x}$)-(x+$\frac{1}{x}$)=a(a2-2)-a=a3-3a,
x4+$\frac{1}{{x}^{4}}$=(x2+$\frac{1}{{x}^{2}}$)2-2=(a2-2)2-2=a4-4a2+2,
x5+$\frac{1}{{x}^{5}}$=(x4+$\frac{1}{{x}^{4}}$)(x+$\frac{1}{x}$)-(x3+$\frac{1}{{x}^{3}}$)=a(a4-4a2+2)-(a3-3a)=a5-5a3+5a,
∴a5-5a3+5a=123,
(a5-3a4)+3(a4-3a3)+4(a3-3a2)+12(a2-3a)+41(a-3)=0,
(a-3)(a4+3a3+4a2+12a+41)=0,
∴a-3=0,
解得a=3,
即x+$\frac{1}{x}$的值為3.
故答案為:3.
點評 考查了換元法解分式方程,利用完全平方公式以及提取公因式法進行分解得出是解題的關(guān)鍵.換元的實質(zhì)是轉(zhuǎn)化,關(guān)鍵是構(gòu)造元和設(shè)元,理論依據(jù)是等量代換,目的是變換研究對象,將問題移至新對象的知識背景中去研究,從而使非標準型問題標準化、復(fù)雜問題簡單化,變得容易處理.


科目:初中數(shù)學(xué) 來源: 題型:解答題
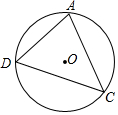 如圖,△ADC內(nèi)接于⊙O.
如圖,△ADC內(nèi)接于⊙O.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5條 | B. | 6條 | C. | 7條 | D. | 8條 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,給正五邊形的頂點依次編號為1,2,3,4,5.若從某一頂點開始,沿正五邊形的邊順時針方向行走,頂點編號的數(shù)字是幾,就走幾個邊長,則稱這種走法為一次“移位”.如:小宇在編號為3的頂點上時,那么他應(yīng)走3個邊長,即從3→4→5→1為第一次“移位”,這時他到達編號為1的頂點;然后從1→2為第二次“移位”.若小宇從編號為2的頂點開始,第20次“移位”后,則他所處頂點的編號為1.
如圖,給正五邊形的頂點依次編號為1,2,3,4,5.若從某一頂點開始,沿正五邊形的邊順時針方向行走,頂點編號的數(shù)字是幾,就走幾個邊長,則稱這種走法為一次“移位”.如:小宇在編號為3的頂點上時,那么他應(yīng)走3個邊長,即從3→4→5→1為第一次“移位”,這時他到達編號為1的頂點;然后從1→2為第二次“移位”.若小宇從編號為2的頂點開始,第20次“移位”后,則他所處頂點的編號為1.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 最大的負整數(shù)為-1 | B. | 最小的正整數(shù)為1 | ||
| C. | 最小的整數(shù)是0 | D. | 相反數(shù)等于它本身的數(shù)是0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com