
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作直線
作直線![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() (點
(點![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ),射線
),射線![]() ,
,![]() 分別交直線
分別交直線![]() 于點
于點![]() ,
,![]() .
.
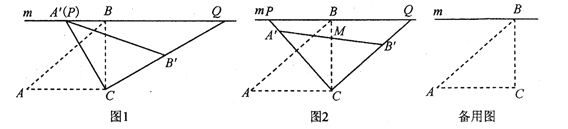
(1)如圖1,當![]() 與
與![]() 重合時,求
重合時,求![]() 的度數;
的度數;
(2)如圖2,設![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 為
為![]() 的中點時,求線段
的中點時,求線段![]() 的長;
的長;
(3)在旋轉過程中,當點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 的延長線上時,試探究四邊形
的延長線上時,試探究四邊形![]() 的面積是否存在最小值.若存在,求出四邊形
的面積是否存在最小值.若存在,求出四邊形![]() 的最小面積;若不存在,請說明理由.
的最小面積;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 的最小值為
的最小值為![]() .
.
【解析】
(1)由旋轉可得:AC=A'C=2,進而得到BC=![]() ,依據∠A'BC=90°,可得
,依據∠A'BC=90°,可得![]() ,即可得到∠A'CB=30°,∠ACA'=60°;
,即可得到∠A'CB=30°,∠ACA'=60°;
(2)根據M為A'B'的中點,即可得出∠A=∠A'CM,進而得到PB=![]() BC=
BC=![]() ,依據tan∠Q=tan∠A=
,依據tan∠Q=tan∠A=![]() ,即可得到BQ=BC×
,即可得到BQ=BC×![]() =2,進而得出PQ=PB+BQ=
=2,進而得出PQ=PB+BQ=![]() ;
;
(3)依據S四邊形PA'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣![]() ,即可得到S四邊形PA'B′Q最小,即S△PCQ最小,而
,即可得到S四邊形PA'B′Q最小,即S△PCQ最小,而![]() ,利用幾何法或代數法即可得到S△PCQ的最小值=3,S四邊形PA'B′Q=3﹣
,利用幾何法或代數法即可得到S△PCQ的最小值=3,S四邊形PA'B′Q=3﹣![]() .
.
解:(1)由旋轉可得:AC=A'C=2,
∵∠ACB=90°,AB=![]() ,AC=2,
,AC=2,
∴BC=![]() ,
,
∵∠ACB=90°,m∥AC,
∴∠A'BC=90°,
∴cos∠A'CB=![]() ,
,
∴∠A'CB=30°,
∴∠ACA'=60°;
(2)∵M為A'B'的中點,
∴∠A'CM=∠MA'C,
由旋轉可得,∠MA'C=∠A,
∴∠A=∠A'CM,
∴tan∠PCB=tan∠A![]() ,
,
∴![]() ,
,
∵∠BQC=∠BCP=∠A,
∴tan∠BQC=tan∠A=![]() ,
,
∴BQ=BC×![]() =2,
=2,
∴PQ=PB+BQ=![]() ;
;
(3)∵S四邊形PA'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣![]() ,
,
∴S四邊形PA'B′Q最小,即S△PCQ最小,
∴![]() ,
,
法一:(幾何法)取PQ的中點G,
∵∠PCQ=90°,
∴CG=![]() PQ,即PQ=2CG,
PQ,即PQ=2CG,
當CG最小時,PQ最小,
∴CG⊥PQ,即CG與CB重合時,CG最小,
∴CGmin=![]() ,PQmin=2
,PQmin=2![]() ,
,
∴S△PCQ的最小值=3,S四邊形PA'B′Q=3﹣![]() ;
;
法二(代數法)設PB=x,BQ=y,
由射影定理得:xy=3,
∴當PQ最小時,x+y最小,
∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,
當x=y=![]() 時,“=”成立,
時,“=”成立,
∴PQ=![]() +
+![]() =2
=2![]() ,
,
∴S△PCQ的最小值=3,S四邊形PA'B′Q=3﹣![]() .
.


科目:初中數學 來源: 題型:
【題目】已知一次函數y=ax+b過一,二,四象限,且過(6,0),則關于二次函數y=ax2+bx+1的以下說法:①圖象與x軸有兩個交點;②a<0,b>0;③當x=3時函數有最小值;④若存在一個實數m,當x≤m時,y隨x的增大而增大,則m≤3.其中正確的是( )
A. ①②B. ①②③C. ①②④D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景(1)如圖1,△ABC中,DE∥BC分別交AB,AC于D,E兩點,過點E作EF∥AB交BC于點F.請按圖示數據填空:△EFC的面積![]() __________,△ADE的面積
__________,△ADE的面積![]() ______________.
______________.
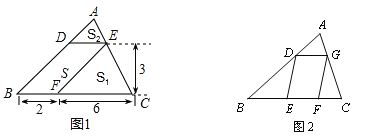
探究發現(2)在(1)中,若BF=m,FC=n,DE與BC間的距離為![]() .請證明
.請證明![]() .
.
拓展遷移(3)如圖2,□DEFG的四個頂點在△ABC的三邊上,若△ADG、△DBE、△GFC的面積分別為3、7、5,試利用(2)中的結論求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
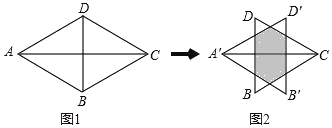
【題目】如圖1,等邊△ABD與等邊△CBD的邊長均為2,將△ABD沿AC方向向右平移k個單位到△A′B′D′的位置,得到圖2,則下列說法:①陰影部分的周長為4;②當k=![]() 時,圖中陰影部分為正六邊形;③當k=
時,圖中陰影部分為正六邊形;③當k=![]() 時,圖中陰影部分的面積是
時,圖中陰影部分的面積是![]() ;正確的是( )
;正確的是( )
A. ①B. ①②C. ①③D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題發現:
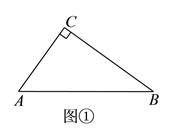
(![]() )如圖①,
)如圖①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上任意一點,則
邊上任意一點,則![]() 的最小值為__________.
的最小值為__________.
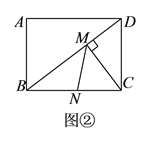
(![]() )如圖②,矩形
)如圖②,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、點
、點![]() 分別在
分別在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
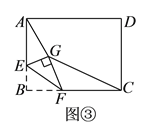
(![]() )如圖③,矩形
)如圖③,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上一點,且
邊上一點,且![]() ,點
,點![]() 是
是![]() 邊上的任意一點,把
邊上的任意一點,把![]() 沿
沿![]() 翻折,點
翻折,點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() 、
、![]() ,四邊形
,四邊形![]() 的面積是否存在最小值,若存在,求這個最小值及此時
的面積是否存在最小值,若存在,求這個最小值及此時![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,
,![]() 為
為![]() 上一點,經過點
上一點,經過點![]() ,
,![]() 的
的![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
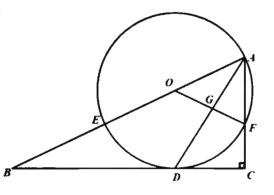
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)設![]() ,
,![]() ,試用含
,試用含![]() 的代數式表示線段
的代數式表示線段![]() 的長;
的長;
(3)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中有一直角三角形AOB,O為坐標原點,OA=1,tan∠BAO=3,將此三角形繞原點O逆時針旋轉90°,得到△DOC,拋物線y=ax2+bx+c經過點A、B、C.
(1)求拋物線的解析式;
(2)若點P是第二象限內拋物線上的動點,其橫坐標為t,設拋物線對稱軸l與x軸交于一點E,連接PE,交CD于F,求以C、E、F為頂點三角形與△COD相似時點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
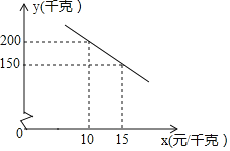
【題目】某農戶承包荒山種植某產品種蜜柚![]() 已知該蜜柚的成本價為8元
已知該蜜柚的成本價為8元![]() 千克,投入市場銷售時,調查市場行情,發現該蜜柚銷售不會虧本,且每天銷量
千克,投入市場銷售時,調查市場行情,發現該蜜柚銷售不會虧本,且每天銷量![]() 千克
千克![]() 與銷售單價
與銷售單價![]() 元
元![]() 千克
千克![]() 之間的函數關系如圖所示.
之間的函數關系如圖所示.
![]() 求y與x的函數關系式,并寫出x的取值范圍;
求y與x的函數關系式,并寫出x的取值范圍;
![]() 當該品種蜜柚定價為多少時,每天銷售獲得的利潤最大?最大利潤是多少?
當該品種蜜柚定價為多少時,每天銷售獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點D在⊙O上,OC∥AD交⊙O于E, 點F在CD延長線上, 且∠BOC+∠ADF=90°.
(1)求證:![]() ;
;
(2)求證:CD是⊙O的切線.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com