
【題目】如圖,在平面直角坐標系中有一直角三角形AOB,O為坐標原點,OA=1,tan∠BAO=3,將此三角形繞原點O逆時針旋轉90°,得到△DOC,拋物線y=ax2+bx+c經過點A、B、C.
(1)求拋物線的解析式;
(2)若點P是第二象限內拋物線上的動點,其橫坐標為t,設拋物線對稱軸l與x軸交于一點E,連接PE,交CD于F,求以C、E、F為頂點三角形與△COD相似時點P的坐標.

【答案】(1)拋物線的解析式為y=﹣x2﹣2x+3;(2)當△CEF與△COD相似時,P點的坐標為(﹣1,4)或(﹣2,3).
【解析】
(1)根據正切函數,可得OB,根據旋轉的性質,可得△DOC≌△AOB,根據待定系數法,可得函數解析式;
(2)分兩種情況討論:①當∠CEF=90°時,△CEF∽△COD,此時點P在對稱軸上,即點P為拋物線的頂點;②當∠CFE=90°時,△CFE∽△COD,過點P作PM⊥x軸于M點,得到△EFC∽△EMP,根據相似三角形的性質,可得PM與ME的關系,解方程,可得t的值,根據自變量與函數值的對應關系,可得答案.
(1)在Rt△AOB中,OA=1,tan∠BAO![]() 3,∴OB=3OA=3.
3,∴OB=3OA=3.
∵△DOC是由△AOB繞點O逆時針旋轉90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A,B,C的坐標分別為(1,0),(0,3),(﹣3,0),代入解析式為
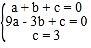 ,解得:
,解得: ,拋物線的解析式為y=﹣x2﹣2x+3;
,拋物線的解析式為y=﹣x2﹣2x+3;
(2)∵拋物線的解析式為y=﹣x2﹣2x+3,∴對稱軸為l![]() 1,∴E點坐標為(﹣1,0),如圖,分兩種情況討論:
1,∴E點坐標為(﹣1,0),如圖,分兩種情況討論:
①當∠CEF=90°時,△CEF∽△COD,此時點P在對稱軸上,即點P為拋物線的頂點,P(﹣1,4);
②當∠CFE=90°時,△CFE∽△COD,過點P作PM⊥x軸于M點,∵∠CFE=∠PME=90°,∠CEF=∠PEM,∴△EFC∽△EMP,∴![]() ,∴MP=3ME.
,∴MP=3ME.
∵點P的橫坐標為t,∴P(t,﹣t2﹣2t+3).
∵P在第二象限,∴PM=﹣t2﹣2t+3,ME=﹣1﹣t,t<0,∴﹣t2﹣2t+3=3(﹣1﹣t),解得:t1=﹣2,t2=3(與t<0矛盾,舍去).
當t=﹣2時,y=﹣(﹣2)2﹣2×(﹣2)+3=3,∴P(﹣2,3).
綜上所述:當△CEF與△COD相似時,P點的坐標為(﹣1,4)或(﹣2,3).


科目:初中數學 來源: 題型:
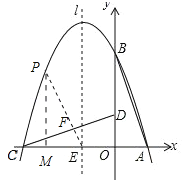
【題目】如圖,在四邊形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分別為AD,CD的中點,連接BE,BF,延長BE交CD的延長線于點M.
(1)求證:四邊形ABCD為矩形;
(2)若MD=6,BC=12,求BF的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1.在△ABC中,矩形EFGH的一邊EF在AB上,頂點G、H分別在BC、AC上,CD是邊AB上的高,CD交GH于點I.若CI=4,HI=3,AD![]() .矩形DFGI恰好為正方形.
.矩形DFGI恰好為正方形.
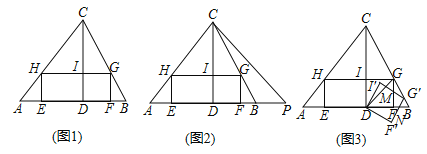
(1)求正方形DFGI的邊長;
(2)如圖2,延長AB至P.使得AC=CP,將矩形EFGH沿BP的方向向右平移,當點G剛好落在CP上時,試判斷移動后的矩形與△CBP重疊部分的形狀是三角形還是四邊形,為什么?
(3)如圖3,連接DG,將正方形DFGI繞點D順時針旋轉一定的角度得到正方形DF′G′I′,正方形DF′G′I′分別與線段DG、DB相交于點M、N,求△MNG′的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,點P由點B出發沿BA方向向點A勻速運動,速度為1cm/s;點Q由點A出發沿AC方向向點C勻速運動,速度為2cm/s;連結PQ。若設運動時間為t(s)(0<t<2),解答下列問題:

(1)當t為何值時?PQ//BC?
(2)設△APQ的面積為y(cm2),求y與t之間的函數關系?
(3)是否存在某一時刻t,使線段PQ恰好把△ABC的周長和面積同時平分?若存在求出此時t的值;若不存在,說明理由。
(4)如圖2,連結PC,并把△PQC沿AC翻折,得到四邊形PQP'C,那么是否存在某一時刻t,使四邊形PQP'C為菱形?若存在求出此時t的值;若不存在,說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 拋物線![]() 與
與![]() 軸交于點A(-1,0),頂點坐標(1,n)與
軸交于點A(-1,0),頂點坐標(1,n)與![]() 軸的交點在(0,2),(0,3)之間(包 含端點),則下列結論:①
軸的交點在(0,2),(0,3)之間(包 含端點),則下列結論:①![]() ;②
;②![]() ;③對于任意實數m,
;③對于任意實數m,![]() 總成立;④關于
總成立;④關于![]() 的方程
的方程![]() 有兩個不相等的實數根.其中結論正確的個數為
有兩個不相等的實數根.其中結論正確的個數為![]()
![]()
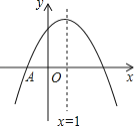
A. 1 個 B. 2 個 C. 3 個 D. 4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 y=ax2+bx+c(a≠0)的圖象如圖,有下列 5 個結論:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的實數);其中正確結論的個數為( )
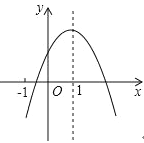
A. 2 個 B. 3 個 C. 4 個 D. 5 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將圖中的A型、B型、C型矩形紙片分別放在3個盒子中,盒子的形狀、大小、質地都相同,再將這3個盒子裝入一只不透明的袋子中.
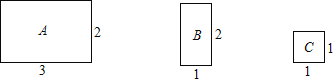
(1)攪勻后從中摸出1個盒子,求摸出的盒子中是![]() 型矩形紙片的概率;
型矩形紙片的概率;
(2)攪勻后先從中摸出1個盒子(不放回),再從余下的兩個盒子中摸出一個盒子,求2次摸出的盒子的紙片能拼成一個新矩形的概率(不重疊無縫隙拼接).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小亮玩一個游戲:三張大小、質地都相同的卡片上分別標有數字2,3,4(背面完全相同),現將標有數字的一面朝下.小明從中任意抽取一張,記下數字后放回洗勻,然后小亮從中任意抽取一張,計算小明和小亮抽得的兩個數字之和.若和為奇數,則小明勝;若和為偶數,則小亮勝.
(1)請你用畫樹狀圖或列表的方法,求出這兩數和為6的概率.
(2)你認為這個游戲規則對雙方公平嗎?說說你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com