
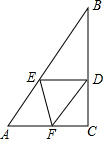
 如圖,Rt△ABC中,∠C=90°,∠B=30°,點D在BC上,BD=2CD,過D點作BC的垂線交AB于點E,BE=6cm,F為線段AC上一動點,則△DEF的周長最小值為9cm.
如圖,Rt△ABC中,∠C=90°,∠B=30°,點D在BC上,BD=2CD,過D點作BC的垂線交AB于點E,BE=6cm,F為線段AC上一動點,則△DEF的周長最小值為9cm. 分析 如圖,作點D關于直線AC的對稱點H,連接EH交AC于F,此時FE+FD的值最小,即△DEF的周長最小.求出DE、EH的長即可解決問題.
解答 解:如圖,作點D關于直線AC的對稱點H,連接EH交AC于F,此時FE+FD的值最小,即△DEF的周長最小.
在Rt△BED中,∵∠EDB=90°,∠B=30°,BE=6cm,
∴DE=3cm<BD=3$\sqrt{3}$cm,
∵BD=2CD,
∴CD=CH=$\frac{3\sqrt{3}}{2}$,
在Rt△EDH中,EH=$\sqrt{D{E}^{2}+D{H}^{2}}$=6cm,
∵FD=FH,
∴△DEF的周長的最小值=DE+EF+DF=DE+EF+FH=EH+DE=6+3=9cm,
故答案為9.
點評 本題考查軸對稱-最短問題、勾股定理等知識,解題的關鍵是學會利用對稱解決最短問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
 在如圖所示的平面直角坐標系中表示下面各點:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如圖所示的平面直角坐標系中表示下面各點:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
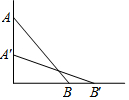 如圖,一根長為a的竹竿AB斜靠在墻上,竹竿AB的傾斜角為α,當竹竿的頂端A下滑到點A'時,竹竿的另一端B向右滑到了點B',此時傾斜角為β.
如圖,一根長為a的竹竿AB斜靠在墻上,竹竿AB的傾斜角為α,當竹竿的頂端A下滑到點A'時,竹竿的另一端B向右滑到了點B',此時傾斜角為β.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
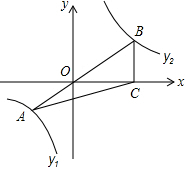 如圖,已知在平面直角坐標系xOy中,O是坐標原點,點A是函數y1=$\frac{4}{x}$(x<0)圖象上一點,AO的延長線交函數y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2圖象于點B,BC⊥x軸,若S△ABC=$\frac{15}{2}$,求函數y2.
如圖,已知在平面直角坐標系xOy中,O是坐標原點,點A是函數y1=$\frac{4}{x}$(x<0)圖象上一點,AO的延長線交函數y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2圖象于點B,BC⊥x軸,若S△ABC=$\frac{15}{2}$,求函數y2.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 已知Rt△DEF按如圖所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,點H為線段FD延長線上一動點,現將△DEH繞點D順時針旋轉60°得到△DAK,E的對應點是A,H的對應點是K,若△EHK的面積為4$\sqrt{3}$,則DH的值為2.
已知Rt△DEF按如圖所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,點H為線段FD延長線上一動點,現將△DEH繞點D順時針旋轉60°得到△DAK,E的對應點是A,H的對應點是K,若△EHK的面積為4$\sqrt{3}$,則DH的值為2.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com