Question

1．如圖：已知反比例函數y=$\frac{{k}_{1}}{x}$與一次函數y=k₂x+b的圖象交于A（2，-1），B（$-\frac{1}{2}，m$）．
（1）求k₁、k₂，b的值；
（2）求三角形AOB的面積；
（3）若M（x₁，y₁），N（x₂，y₂）是反比例函數y=$\frac{{k}_{1}}{x}$圖象上的兩點，且x₁＜x₂，y₁＞y₂，指出M、N各位于哪個象限，并簡單說明理由．

Answer 1

分析 （1）先把A點坐標代入y=$\frac{{k}_{1}}{x}$可求出k₁=-2，則反比例函數的解析式為y=-$\frac{2}{x}$，再把B（$-\frac{1}{2}，m$）代入反比例函數解析式求出m，得到B點坐標，然后利用待定系數法求一次函數解析式即可；
（2）如圖，設直線AB交y軸于C點，則C（0，3），然后根據三角形面積公式，利用S_△AOB=S_△AOC+S_△BOC進行計算；
（3）根據反比例函數的性質，在每一象限內y隨x的增大而增大，而x₁＜x₂，y₁＞y₂，于是可判斷M點和N點不在同一象限，則易得點M在第二象限，點N在第四象限．

解答 解：（1）把A（2，-1）代入y=$\frac{{k}_{1}}{x}$得k₁=2×（-1）=-2，
則反比例函數的解析式為y=-$\frac{2}{x}$
把B（$-\frac{1}{2}，m$）代入y=-$\frac{2}{x}$得-$\frac{1}{2}$m=-2，解得m=4，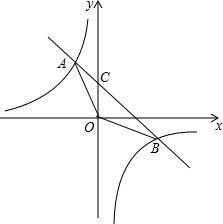
把A（2，-1）、B（-$\frac{1}{2}$，4）代入y=k₂x+b得$\left\{\begin{array}{l}{2{k}_{2}+b=-1}\\{-\frac{1}{2}{k}_{2}+b=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{{k}_{2}=-2}\\{b=3}\end{array}\right.$，
則直線解析式為y=-2x+3，
即k₁、k₂，b的值分別為-2，-2，3；
（2）如圖，設直線AB交y軸于C點，
當x=0時，y=-2x+3=3，則C（0，3），
所以S_△AOB=S_△AOC+S_△BOC=$\frac{1}{2}$×3×$\frac{1}{2}$+$\frac{1}{2}$×3×2=$\frac{15}{4}$；
（3）因為M（x₁，y₁），N（x₂，y₂）是反比例函數y=-$\frac{2}{x}$圖象上的兩點，且x₁＜x₂，y₁＞y₂，
所以M點和N點不在同一象限，其中點M在第二象限，點N在第四象限．

點評 本題考查了反比例函數與一次函數的交點問題：求反比例函數與一次函數的交點坐標，把兩個函數關系式聯立成方程組求解，若方程組有解則兩者有交點，方程組無解，則兩者無交點．也考查了反比例函數的性質．