Question

1．⊙O是△ABC的外接圓，AB是直徑，過$\widehat{BC}$的中點P作⊙O的直徑PG交弦BC于點D，連接AG，CP，PB．

（1）如題圖1；若D是線段OP的中點，求∠BAC的度數；
（2）如題圖2，在DG上取一點k，使DK=DP，連接CK，求證：四邊形AGKC是平行四邊形；
（3）如題圖3，取CP的中點E，連接ED并延長ED交AB于點H，連接PH，求證：PH⊥AB．

Answer 1

分析 （1）如圖1，根據垂徑定理得到PG⊥BC，則BD垂直平分OP，于是可判斷△OBP為等邊三角形，所以∠BOP=60°，然后估計圓周角定理得到∠BAC=∠BOP=60°；
（2）連接KB，GB、PA，如圖2，先判定四邊形BPCK為平行四邊形得到PB=CK，PB∥CK，再判斷四邊形APBG為平行四邊形得到PB=AG，PB∥AG，則CK=AG，CK∥AG然后判斷四邊形AGCK是平行四邊形；
（3）如圖3，先估計三角形中位線性質得DE∥PB，即DH∥PB，再判定△ODH為等腰三角形得到OD=OH，接著證明△OBD≌△HOP，則∠OHP=∠ODB=90°．所以PH⊥AB．

解答 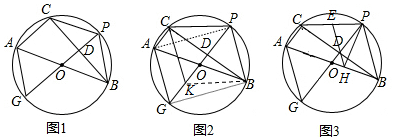（1）解：如圖1，
∵AB為⊙O直徑，點P是$\widehat{BC}$的中點，
∴PG⊥BC，即∠ODB=90°．
∵D為OP的中點，
∴BD垂直平分OP，
∴BP=BO，
而OB=OP，
∴△OBP為等邊三角形，
∴∠BOP=60°，
∴∠BAC=∠BOP=60°；
（2）證明：連接KB，GB、PA，如圖2，
由（1）知，CD=BD，
∵DK=DP，
∴四邊形BPCK為平行四邊形，
∴PB=CK，PB∥CK，
∵PA=OB，OG=OP，
∴四邊形APBG為平行四邊形，
∴PB=AG，PB∥AG，
∴CK=AG，CK∥AG，
∴四邊形AGCK是平行四邊形；
（3）證明：如圖3，
∵CE=PE，CD=BD，
∴DE∥PB，即DH∥PB，
而△OPB為等腰三角形，
∴△ODH為等腰三角形，
∴OD=OH，
在△ODB和△OHP中
$\left\{\begin{array}{l}{OD=OH}\\{∠BOD=∠POH}\\{OB=OP}\end{array}\right.$，
∴△OBD≌△HOP（SAS），
∴∠OHP=∠ODB，
而BC⊥DG，
∴∠OHP=∠ODB=90°．
∴PH⊥AB．

點評 本題考查了圓的綜合題：熟練掌握垂徑定理、圓周角定理和等邊三角形的判定與性質；靈活應用平行四邊形的判定與性質；會應用全等三角形的知識解決角相等的問題．