Question

2．如圖，已知點A（1，$\sqrt{3}$）在反比例函數(shù)y=$\frac{k}{x}$（x＞0）的圖象上，連接OA，將線段OA繞點O沿順時針方向旋轉(zhuǎn)30°，得到線段OB．
（1）求反比例函數(shù)的解析式；
（2）填空：
①點B的坐標是（1，$\sqrt{3}$）；
②判斷點B是否在反比例函數(shù)的圖象上？答點B在反比例函數(shù)的圖象上；
③設直線AB的解析式為y=ax+b，則不等式ax+b-$\frac{k}{x}$＜0的解集是0＜x＜1或x＞$\sqrt{3}$．

Answer 1

分析 （1）把A點坐標代入反比例函數(shù)解析式可求得k，可求得其解析式；
（2）①由A點坐標可求得OA，由旋轉(zhuǎn)性質(zhì)可求得OB，由A點坐標可求得OA與x軸的夾角，則可求得OB與x軸的夾角，可求得B點坐標；②把B點坐標代入反比例函數(shù)解析式進行判斷即可；③結(jié)合圖象可知不等式的解集即為直線AB在反比例函數(shù)圖象下方時對應的x的取值范圍，可求得答案．

解答 解：
（1）∵點A（1，$\sqrt{3}$）在反比例函數(shù)y=$\frac{k}{x}$（x＞0）的圖象上，
∴$\sqrt{3}$=$\frac{k}{1}$，解得k=$\sqrt{3}$，
∴反比例函數(shù)的解析式為y=$\frac{\sqrt{3}}{x}$（x＞0）；
（2）①如圖，過A作AC⊥x軸于點C，過B作BD⊥x軸于點D，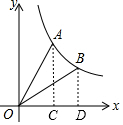

∵A（1，$\sqrt{3}$），
∴OC=1，AC=$\sqrt{3}$，
∴tan∠AOC=$\frac{AC}{OC}$=$\sqrt{3}$，OA=2，
∴∠AOC=60°，
∵將線段OA繞點O沿順時針方向旋轉(zhuǎn)30°，得到線段OB，
∴OB=2，∠BOD=30°，
∴BD=$\frac{1}{2}$OB=1，OD=$\frac{\sqrt{3}}{2}$OB=$\sqrt{3}$，
∴B（1，$\sqrt{3}$），
故答案為：（1，$\sqrt{3}$）；
②∵$\sqrt{3}$×1=$\sqrt{3}$，
∴點B在反比例函數(shù)的圖象上，
故答案為：點B在反比例函數(shù)的圖象上；
③∵ax+b-$\frac{k}{x}$＜0可化為ax+b＜$\frac{k}{x}$，
∴不等式的解集為直線AB在反比例函數(shù)圖象的下方，
∴0＜x＜1或x＞$\sqrt{3}$，
故答案為：0＜x＜1或x＞$\sqrt{3}$．

點評 本題為反比例函數(shù)的綜合應用，涉及待定系數(shù)法、旋轉(zhuǎn)的性質(zhì)、三角函數(shù)的定義及數(shù)形結(jié)合思想．在（1）中注意函數(shù)圖象上的點的坐標滿足函數(shù)解析式，在（2）中求得B點坐標是解題的關鍵．本題考查知識點較多，綜合性較強，難度適中．