
【題目】在平面直角坐標系中,已知拋物線![]() (b,c為常數)的頂點為P,等腰直角三角形ABC的頂點A的坐標為(0,﹣1),C的坐標為(4,3),直角頂點B在第四象限.
(b,c為常數)的頂點為P,等腰直角三角形ABC的頂點A的坐標為(0,﹣1),C的坐標為(4,3),直角頂點B在第四象限.
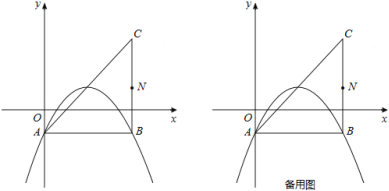
(1)如圖,若該拋物線過A,B兩點,求該拋物線的函數表達式;
(2)平移(1)中的拋物線,使頂點P在直線AC上滑動,且與AC交于另一點Q.
(i)若點M在直線AC下方,且為平移前(1)中的拋物線上的點,當以M、P、Q三點為頂點的三角形是等腰直角三角形時,求出所有符合條件的點M的坐標;
(ii)取BC的中點N,連接NP,BQ.試探究![]() 是否存在最大值?若存在,求出該最大值;若不存在,請說明理由.
是否存在最大值?若存在,求出該最大值;若不存在,請說明理由.
【答案】解:(1)由題意,得點B的坐標為(4,﹣1).
∵拋物線過A(0,﹣1),B(4,﹣1)兩點,
∴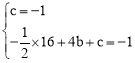 ,解得
,解得![]() 。
。
∴拋物線的函數表達式為:![]() 。
。
(2)(i)∵A(0,﹣1),C(4,3),∴直線AC的解析式為:y=x﹣1。
設平移前拋物線的頂點為P0,則由(1)可得P0的坐標為(2,1),且P0在直線AC上。
∵點P在直線AC上滑動,∴可設P的坐標為(m,m﹣1)。
則平移后拋物線的函數表達式為:![]() 。
。
解方程組: ,解得
,解得![]() ,
,![]() 。
。
∴P(m,m﹣1),Q(m﹣2,m﹣3)。
過點P作PE∥x軸,過點Q作QE∥y軸,則
PE=m﹣(m﹣2)=2,QE=(m﹣1)﹣(m﹣3)=2,
∴PQ=![]() =AP0。
=AP0。
若△MPQ為等腰直角三角形,則可分為以下兩種情況:
①當PQ為直角邊時:點M到PQ的距離為![]() (即為PQ的長),
(即為PQ的長),
由A(0,﹣1),B(4,﹣1),P0(2,1)可知,
△ABP0為等腰直角三角形,且BP0⊥AC,BP0=![]() 。
。
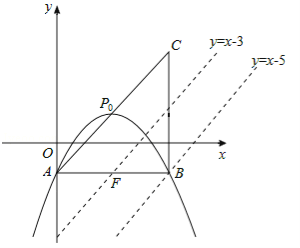
如答圖1,過點B作直線l1∥AC,交拋物線![]() 于點M,則M為符合條件的點。
于點M,則M為符合條件的點。
∴可設直線l1的解析式為:y=x+b1。
∵B(4,﹣1),∴﹣1=4+b1,解得b1=﹣5。∴直線l1的解析式為:y=x﹣5。
解方程組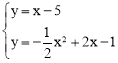 ,得:
,得:![]() ,
,![]() 。
。
∴M1(4,﹣1),M2(﹣2,﹣7)。
②當PQ為斜邊時:MP=MQ=2,可求得點M到PQ的距離為![]() .
.
如答圖1,取AB的中點F,則點F的坐標為(2,﹣1)。
由A(0,﹣1),F(2,﹣1),P0(2,1)可知:
△AFP0為等腰直角三角形,且點F到直線AC的距離為![]() 。
。
過點F作直線l2∥AC,交拋物線![]() 于點M,則M為符合條件的點。
于點M,則M為符合條件的點。
∴可設直線l2的解析式為:y=x+b2,
∵F(2,﹣1),∴﹣1=2+b2,解得b1=﹣3。∴直線l2的解析式為:y=x﹣3。
解方程組 ,得:
,得: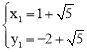 ,
,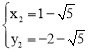 。
。
∴M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() )。
)。
綜上所述,所有符合條件的點M的坐標為:
M1(4,﹣1),M2(﹣2,﹣7),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() )。
)。
(ii)![]() 存在最大值。理由如下:
存在最大值。理由如下:
由(i)知PQ=![]() 為定值,則當NP+BQ取最小值時,
為定值,則當NP+BQ取最小值時,![]() 有最大值。
有最大值。
如答圖2,取點B關于AC的對稱點B′,易得點B′的坐標為(0,3),BQ=B′Q。
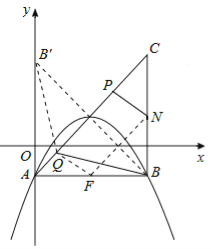
連接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四邊形PQFN為平行四邊形。
∴NP=FQ。
∴NP+BQ=FQ+B′P≥FB′![]() 。
。
∴當B′、Q、F三點共線時,NP+BQ最小,最小值為![]() 。
。
∴![]() 的最大值為
的最大值為![]() 。
。
【解析】(1)先求出點B的坐標,然后利用待定系數法求出拋物線的函數表達式。
(2)(i)首先求出直線AC的解析式和線段PQ的長度,作為后續計算的基礎。
若△MPQ為等腰直角三角形,則可分為以下兩種情況:
①當PQ為直角邊時:點M到PQ的距離為![]() .此時,將直線AC向右平移4個單位后所得直線(y=x﹣5)與拋物線的交點,即為所求之M點。
.此時,將直線AC向右平移4個單位后所得直線(y=x﹣5)與拋物線的交點,即為所求之M點。
②當PQ為斜邊時:點M到PQ的距離為![]() .此時,將直線AC向右平移2個單位后所得直線(y=x﹣3)與拋物線的交點,即為所求之M點.
.此時,將直線AC向右平移2個單位后所得直線(y=x﹣3)與拋物線的交點,即為所求之M點.
(ii)由(i)可知,PQ=![]() 為定值,因此當NP+BQ取最小值時,
為定值,因此當NP+BQ取最小值時,![]() 有最大值。如答圖2所示,作點B關于直線AC的對稱點B′,由解析可知,當B′、Q、F(AB中點)三點共線時,NP+BQ最小,最小值為線段B′F的長度。
有最大值。如答圖2所示,作點B關于直線AC的對稱點B′,由解析可知,當B′、Q、F(AB中點)三點共線時,NP+BQ最小,最小值為線段B′F的長度。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過
經過![]() 兩點.
兩點.
(1)求這個二次函數的表達式;
(2)若![]() 是直線
是直線![]() 上方拋物線上一點;
上方拋物線上一點;
①當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
②在①的條件下,點![]() 關于拋物線對稱軸的對稱點為
關于拋物線對稱軸的對稱點為![]() ,在直線
,在直線![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與直線
與直線![]() 的夾角是
的夾角是![]() 的兩倍,若存在,直接寫出點
的兩倍,若存在,直接寫出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+4ax+c(a≠0)的圖象交x軸于A、B兩點(A在B的左側),交y軸于點C.一次函數y=﹣![]() x+b的圖象經過點A,與y軸交于點D(0,﹣3),與這個二次函數的圖象的另一個交點為E,且AD:DE=3:2.
x+b的圖象經過點A,與y軸交于點D(0,﹣3),與這個二次函數的圖象的另一個交點為E,且AD:DE=3:2.
(1)求這個二次函數的表達式;
(2)若點M為x軸上一點,求MD+![]() MA的最小值.
MA的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
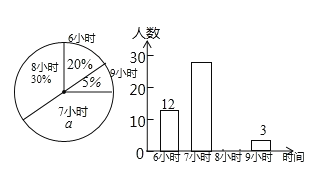
【題目】為了了解某校初中各年級學生每天的平均睡眠時間(單位:h,精確到1h),抽樣調查了部分學生,并用得到的數據繪制了下面兩幅不完整的統計圖.
請你根據圖中提供的信息,回答下列問題:
(1)求出扇形統計圖中百分數a的值為 ,所抽查的學生人數為 .
(2)求出平均睡眠時間為8小時的人數,并補全頻數直方圖.
(3)求出這部分學生的平均睡眠時間的眾數和平均數.
(4)如果該校共有學生1200名,請你估計睡眠不足(少于8小時)的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小微企業為加快產業轉型升級步伐,引進一批A,B兩種型號的機器.已知一臺A型機器比一臺B型機器每小時多加工2個零件,且一臺A型機器加工80個零件與一臺B型機器加工60個零件所用時間相等.
(1)每臺A,B兩種型號的機器每小時分別加工多少個零件?
(2)如果該企業計劃安排A,B兩種型號的機器共10臺一起加工一批該零件,為了如期完成任務,要求兩種機器每小時加工的零件不少于72件,同時為了保障機器的正常運轉,兩種機器每小時加工的零件不能超過76件,那么A,B兩種型號的機器可以各安排多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知雙曲線y=![]() (x<0)和 y=
(x<0)和 y=![]() (x>0),直線OA與雙曲線y=
(x>0),直線OA與雙曲線y=![]() 交于點A,將直線OA向下平移與雙曲線y=
交于點A,將直線OA向下平移與雙曲線y=![]() 交于點B,與y軸交于點P,與雙曲線y=
交于點B,與y軸交于點P,與雙曲線y=![]() 交于點C,S△ABC=6,
交于點C,S△ABC=6,![]() ,則k=_____.
,則k=_____.
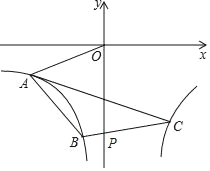
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E在邊CD上(不與點C,D重合),連接AE,BD交于點F.
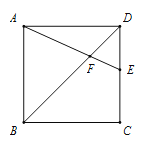
(1)若點E為CD中點,AB=2![]() ,求AF的長.
,求AF的長.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若點G在線段BF上,且GF=2BG,連接AG,CG,設![]() =x,四邊形AGCE的面積為
=x,四邊形AGCE的面積為![]() ,
,![]() ABG的面積為
ABG的面積為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,請在下列四個關系中,選出兩個恰當的關系作為條件,推出四邊形ABCD是平行四邊形,并予以證明.(寫出一種即可)
關系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四邊形ABCD中, , ;
求證:四邊形ABCD是平行四邊形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com