
如圖所示,在Rt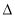 ABC中,∠C=90°,∠BAC=60°,AB=8.半徑為
ABC中,∠C=90°,∠BAC=60°,AB=8.半徑為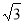 的⊙M與射線BA相切,切點為N,且AN=3.將Rt
的⊙M與射線BA相切,切點為N,且AN=3.將Rt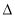 ABC順時針旋轉120
ABC順時針旋轉120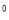 后得到Rt
后得到Rt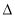 ADE,點B、C的對應點分別是點D、E.
ADE,點B、C的對應點分別是點D、E.
(1)畫出旋轉后的Rt ADE;
ADE;
(2)求出Rt ADE的直角邊DE被⊙M截得的弦PQ的長度;
ADE的直角邊DE被⊙M截得的弦PQ的長度;
(3)判斷Rt ADE的斜邊AD所在的直線與⊙M的位置關系,并說明理由.
ADE的斜邊AD所在的直線與⊙M的位置關系,并說明理由.
(1)作圖見解析;(2)2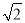 .(3)AD與⊙M相切.理由見解析.
.(3)AD與⊙M相切.理由見解析.
【解析】
試題分析:(1)把三角形ABC繞A旋轉120°就能得到圖形.
(2)連接MQ,過M點作MF⊥DE,由AN=3,AC=4,求出NE的長;在Rt△MFQ中,利用勾股定理可求出QF,根據垂徑定理知QF就是弧長PQ的一半.
(3)過M作AD的垂線設垂足為H,然后證MH與⊙M半徑的大小關系即可;連接AM、MN,由于AE是⊙M的切線,故MN⊥AE,在Rt△AMN中,通過解直角三角形,易求得∠MAN=30°,由此可證得AM是∠DAE的角平分線,根據角平分線的性質即可得到MH=MN,由此可證得⊙M與AD相切.
試題解析:(1)如圖Rt△ADE就是要畫的圖形
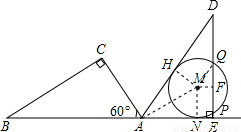
(2)連接MQ,過M點作MF⊥DE,垂足為F,由Rt△ABC可知,NE=1,
在Rt△MFQ中,解得FQ=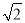 ,故弦PQ的長度2
,故弦PQ的長度2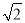 .
.
(3)AD與⊙M相切.
證明:過點M作MH⊥AD于H,連接MN,MA,則MN⊥AE,且MN=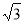 ,
,
在Rt△AMN中,tan∠MAN=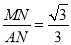 ,
,
∴∠MAN=30°,
∵∠DAE=∠BAC=60°,
∴∠MAD=30°,
∴∠MAN=∠MAD=30°,
∴MH=MN,
∴AD與⊙M相切.
考點:1.切線的判定;2.作圖-旋轉變換.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,正方形網格中,ΔABC 的頂點及點 在格點上。
在格點上。

(1)畫出與ΔABC 關于點O對稱的Δ ;
;
(2)畫出一個以點O為位似中心的Δ ,使得Δ
,使得Δ 與 Δ
與 Δ 的位似比為2。
的位似比為2。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖,已知DE//BC,AB=14,AC=18,AE=10則AD的長為( )
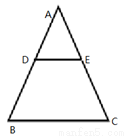
A.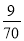 B.
B.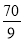 C.
C.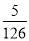 D.
D.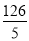
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列各組中的四條線段成比例的是( )
A.4cm,2cm,1cm,3cm
B.1cm,2cm,3cm,5cm
C.3cm,4cm,5cm,6cm
D.1cm,2cm,2cm,4cm
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江西省九年級上學期第二次月考數學試卷(解析版) 題型:解答題
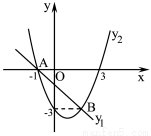
如圖,A(-1,0),B(2,-3)兩點都在一次函數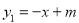 與二次函數
與二次函數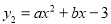 的圖象上.
的圖象上.
(1)求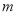 和
和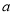 ,
,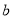 的值;
的值;
(2)請直接寫出當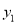 >
>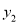 時,自變量
時,自變量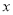 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江西省九年級上學期第二次月考數學試卷(解析版) 題型:填空題
如下圖,△ABC中,∠C=30°.將△ABC繞點A順時針旋轉60°得到△ADE,AE與BC交于F,則∠AFB= °.

查看答案和解析>>
科目:初中數學 來源:2013-2014學年湖北省咸寧市九年級上學期第四次月考數學試卷(解析版) 題型:解答題
(12分)已知關于x的方程 .
.
(1)求證:無論m取任何實數時,方程恒有實數根;(3分)
(2)若關于x的二次函數 的圖象與x軸兩交點間的距離為2時,求拋物線的解析式。(4分)
的圖象與x軸兩交點間的距離為2時,求拋物線的解析式。(4分)
(3)在同一直角坐標系xOy中,畫出(2)中所有函數圖象,結合圖象回答問題:當直線 與(2)中的這個函數圖象只有兩個交點時,求b的取值范圍。(5分)
與(2)中的這個函數圖象只有兩個交點時,求b的取值范圍。(5分)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com