Question

6．如圖，在△ABC中，AB=AC=10m，BC=16m，現點P從點B出發，沿BC向C點運動，運動速度為$\frac{1}{4}$m/s，若點P的運動時間為t秒，則當△ABP是直角三角形時，時間t的值為32s或50s．

Answer 1

分析 分∠APB與∠PAB兩種情況進行分類討論，當∠APB=90°時，AP⊥BC，根據等腰三角形的性質可得出BP=CP，故可得出t的值；當∠PAB=90°時，過點A作AE⊥BC交BC于點E，由等腰三角形的性質得出BE=CE，用t表示出PE的長，再由勾股定理即可得出結論．

解答 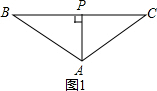解：如圖1，當∠APB=90°時，AP⊥BC，
∵AB=AC，AP⊥BC，
∴BP=CP=$\frac{1}{2}$BC=8cm，
∴$\frac{1}{4}$t=8，解得t=32秒；
如圖2，當∠PAB=90°時，過點A作AE⊥BC交BC于點E，
∵AB=AC，AE⊥BC=8，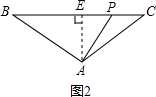
∴BE=CE=$\frac{1}{2}$BC=8，
∴PE=BP-BE=$\frac{1}{4}$t-8．
在Rt△AEC中，AE²=AC²-CE²，即AE²=10²-8²，解得AE=6cm，
在Rt△PAB中，AP²=BP²-AB²，
在Rt△AEP中，AE²=PE²+AE²，
∴（$\frac{1}{4}$t）²-100=（$\frac{1}{4}$t-8）²+36，解得t=50（秒）．
綜上所述，t的值為32秒或50秒．
故答案為：32s或50s．

點評 本題考查的是勾股定理，在解答此題時要注意進行分類討論，不要漏解．