
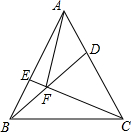
 如圖,已知在等邊△ABC中,AB=AC=BC=8,點D、E分別是邊AC、AB上兩點,且AE=CD,BD交CE于F,連接AF,則AF的最小值為$\frac{8\sqrt{3}}{3}$.
如圖,已知在等邊△ABC中,AB=AC=BC=8,點D、E分別是邊AC、AB上兩點,且AE=CD,BD交CE于F,連接AF,則AF的最小值為$\frac{8\sqrt{3}}{3}$. 分析 由△CAE≌△BCD,推出∠ACE=∠CBD,由∠DFC=∠CBD+∠BCE=∠ACE+∠BCE=60°,推出∠BFC=120°=定值,推出動點F在以O為圓心,OC為半徑的圓弧上,此時∠BOC=120°,連接AO,交BC于G,交⊙O于F′,則易知OB=$\frac{8\sqrt{3}}{3}$,AO=2OB=$\frac{16\sqrt{3}}{3}$,當點F與點F′重合時,AF的值最小,由此即可解決問題.
解答 解:如圖,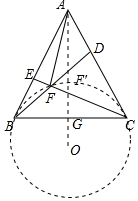
∵△ABC是等邊三角形,
∴AC=BC,∠CAE=∠BCD=60°,
在△CAE和△BCD中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACE=∠BCD}\\{AE=CD}\end{array}\right.$,
∴△CAE≌△BCD,
∴∠ACE=∠CBD,
∵∠DFC=∠CBD+∠BCE=∠ACE+∠BCE=60°,
∴∠BFC=120°=定值,
∴動點F在以O為圓心,OC為半徑的圓弧上,此時∠BOC=120°,連接AO,交BC于G,交⊙O于F′,
則易知OB=$\frac{8\sqrt{3}}{3}$,AO=2OB=$\frac{16\sqrt{3}}{3}$,當點F與點F′重合時,AF的值最小,最小值為$\frac{8\sqrt{3}}{3}$.
故答案為$\frac{8\sqrt{3}}{3}$.
點評 本題考查全等三角形的判定和性質、等邊三角形的性質、圓的有關知識,解題的關鍵是正確探究動點F的運動軌跡,學會利用輔助圓解決問題,屬于中考填空題中的壓軸題.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源:2017屆山東省文慧學校九年級下學期第一次月考數學試卷(解析版) 題型:填空題
如圖,將矩形ABCD沿GH對折,點C落在Q處,點D落在AB邊上E處,EQ與BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,則△EBF的周長是______________ cm.

查看答案和解析>>
科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:單選題
下列四組條件中,不能判定四邊形ABCD是平行四邊形的是( )
A. AB=DC,AD=BC B. AB∥DC,AD∥BC,
C. AB∥DC,AD=BC D. AB∥DC,AB=DC
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
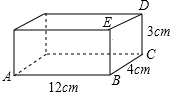 如圖是一個長、寬、高分別為12cm,4cm,3cm的木箱,在它里面放入一根細木條(木條的粗細忽略不計),要求木條不能露出木箱,請你算一算,能放入的細木條的最大長度是多少?
如圖是一個長、寬、高分別為12cm,4cm,3cm的木箱,在它里面放入一根細木條(木條的粗細忽略不計),要求木條不能露出木箱,請你算一算,能放入的細木條的最大長度是多少?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a=2,b=3 | B. | a=2,b=-3 | C. | a=-2,b=3 | D. | a=-2,b=-3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 閱讀材料:
閱讀材料:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com