
如圖,在△ABC中,∠ACB=90°,E為BC上一點,以CE為直徑作⊙O,AB與⊙O相切于點D,連接CD,若BE=OE=2.
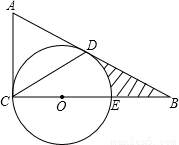
(1)求證:∠A=2∠DCB;
(2)求圖中陰影部分的面積(結果保留π和根號).
(1)證明見解析;(2)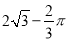 .
.
【解析】
試題分析:(1)連接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度數,關鍵三角形內角和定理求出∠A,即可得出答案;
(2)根據勾股定理求出BD,分別求出△ODB和扇形DOE的度數,即可得出答案.
試題解析:(1)證明:連接OD,
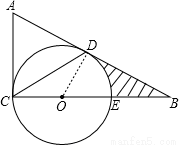
∵AB是⊙O切線,
∴∠ODB=90°,
∴BE=OE=OD=2,
∴∠B=30°,∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC=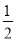 ∠DOB=30°,
∠DOB=30°,
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=2∠DCB;
(2)【解析】
∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2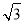 ,
,
∴陰影部分的面積S=S△ODB-S扇形DOE=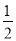 ×2
×2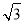 ×2-
×2-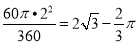 .
.
考點:1.切線的性質;2.扇形面積的計算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:解答題
如圖,矩形ABCD中,AB=12cm,AD=16cm,動點E、F分別從A點、C點同時出發,均以2cm/s的速度分別沿AD向D點和沿CB向B點運動。

(1)經過幾秒首次可使EF⊥AC?
(2)若EF⊥AC,在線段AC上,是否存在一點P,使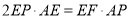 ?若存在,請說明P點的位置,并予以證明;若不存在,請說明理由。
?若存在,請說明P點的位置,并予以證明;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:選擇題
如圖,AB是⊙O的直徑,AD=DE,AE與BD交于點C,則圖中與∠BCE相等的角有
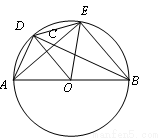
A.2個 B.3個 C.4個 D.5 個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:選擇題
在平面直角坐標系中,若點P(m-3,m+1)在第二象限,則m的取值范圍為
A.-1<m<3 B.m>3 C.m<-1 D.m>-1
查看答案和解析>>
科目:初中數學 來源:2014-2015學年內蒙古化德縣第三中學九年級上學期期末測試數學試卷(解析版) 題型:填空題
已知a,b是方程x2-x-3=0的兩個根,則代數式a2+b+3的值為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年內蒙古化德縣第三中學九年級上學期期末測試數學試卷(解析版) 題型:填空題
開口向上的拋物線y=a(x+2)(x-8)與x軸交于A,B兩點,與y軸交于點C,若∠ACB=90°,則a= .
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在四邊形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中點,∠AED=120°,求證:AB+CD+
如圖,在四邊形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中點,∠AED=120°,求證:AB+CD+| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com