
如果兩個二次函數圖象的開口向上,頂點坐標都相同,那么稱這兩個二次函數互為“同簇二次函數”,顯然“同簇二次函數”不是唯一的.
(1)已知二次函數y=3x2﹣6x+1.
①寫出它的開口方向,頂點坐標;
②請寫出它的兩個不同的“同簇二次函數”.
(2)已知兩個二次函數y1=a1(x﹣k1)2+h1,y2=a2(x﹣k2)2+h2是“同簇二次函數”,則a1a2 0,k1 k2,h1 h2(均填“>”、“=“、或“<”號)
①如果y3=y1+y2也是y1的“同簇二次函數”,求證:y3的頂點在x軸上;
②如果直線y=t,與y1、y2順次交于點A、B、C、D,且AB=BC=CD,求
 的值.
的值.
【考點】二次函數綜合題.
【分析】(1)①由a>0,可判斷出拋物線的開口方向,然后利用配方法可求得拋物線的頂點坐標;
②由“同簇二次函數”的定義寫出兩個頂點坐標為(1,﹣2),a≠3的二次函數即可;
(2)由同簇二次函數可知a1>0,a2>0,k1=k2,h1=h2;
①列出關于y3的函數關系式,然后依據“同簇二次函數”的定義可求得h1=0,從而可求得y3的頂點在x軸上;
②分別求得y1=a1(x﹣k1)2+h1與y=t、y2=a2(x﹣k1)2+h1與y=t的交點橫坐標,最后依據AD=3BC可求得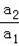
 的值.
的值.
【解答】解:(1)①∵a=3>0,
∴拋物線的開口向上.
∵y=3x2﹣6x+1=3(x﹣1)2﹣2,
∴拋物線的頂點坐標為(1,﹣2).
②由“同簇二次函數”的定義可知y1=2(x﹣1)2﹣2,y2=(x﹣1)2﹣2均是y=3x2﹣6x+1的同簇二次函數.
(2)∵由同簇二次函數可知a1>0,a2>0,k1=k2,h1=h2,
∴a1a2>0,k1=k2,h1=h2.
故答案為:>,=,=.
①∵y3=y1+y2,
∴y3=a1(x﹣k1)2+h1+a2(x﹣k2)2+h2.
∵k1=k2,h1=h2,
∴y3=(a1+a2)(x﹣k1)2+2h1.
∵y3與y1互為同簇二次函數.
∴2h1=h1.
解得h1=0.
∴y3=(a1+a2)(x﹣k1)2.
∴y3的頂點在x軸上.
②將y1=a1(x﹣k1)2+h1與y=t聯立解得:x=k1±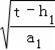
 .
.
將y2=a2(x﹣k1)2+h1與y=t聯立解得:x=k1±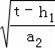
 .
.
∵AB=BC=CD,
∴AD=3BC.
∴2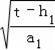
 =6
=6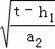
 .
.
解得: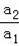
 =9.
=9.
【點評】本題主要考查的是二次函數的綜合應用,解答本題主要應用了配方法求二次函數的頂點坐標、函數圖象的交點與方程組的關系、理解同簇二次函數的概念是解題的關鍵.


科目:初中數學 來源: 題型:
一名射擊運動員連續射靶10次,其中2次命中10環,2次命中9環 ,6次命中8環.則下列說法正確的是 ( )
,6次命中8環.則下列說法正確的是 ( )
A.命中環數的平均數是9 B.命中環數的中位數是9
C.命中環數的眾數是10 D.命中環數的眾數和中位數是8[來源:Z#xx#k.Com]
查看答案和解析>>
科目:初中數學 來源: 題型:
某居民小區開 展節約用電活動,對該
展節約用電活動,對該 小區100戶家庭的節電量情況進行了統計, 4月份與3月份相比,節電情況如下表:
小區100戶家庭的節電量情況進行了統計, 4月份與3月份相比,節電情況如下表:
| 節電量(千瓦時) |
| 30 | 40 | 50 |
| 戶 數 | 10 | 40 | 30 | 20 |
則4月份這100戶節電量的平均數、中位數、眾數分別是( )
A. 35、35、30 B. 25、30、20 C. 36、35、30 D. 36、30、30
查看答案和解析>>
科目:初中數學 來源: 題型:
在期末成績統計表上,小征、小玲、小明三人成績如下:

(1)三人期末 考試的平均成績是多少?
考試的平均成績是多少?
(2)如 果把平時成績、單元測試和期末考試這三個成績按2:3:5的比例計算三人的總評成績,那么三人的總評成績各是多少?
果把平時成績、單元測試和期末考試這三個成績按2:3:5的比例計算三人的總評成績,那么三人的總評成績各是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,△ABC是⊙O的內接三角形,∠BAD是它的一個外角,OP⊥BC交⊙O于點P,僅用直尺按下列要求分別畫圖:
(1)在圖1中,畫并標出△ABC的中線AE;
(2)在圖2中,畫并標出△ABC的角平分線AF;
(3)在圖3中,畫并標出△ABC的外角∠BAD的角平分線AG.


查看答案和解析>>
科目:初中數學 來源: 題型:
我市某中學舉行“中國夢•校園好聲音”歌手大賽,高、初中部根據初賽成績,各選出5名選手組成初中代表隊和高中代表隊參加學校決賽.兩個隊各選出的5名選手的決賽成績如圖所示.
(1)根據圖示填寫下表;

(2)結合兩隊成績的平均數和中位數,分析哪個隊的決賽成績較好;
(3)計算兩隊決賽成績的方差并判斷哪一個代表隊選手成績較為 穩定.
穩定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com