
 如圖,已知等邊△ABC的邊長為8,點D為AC的中點,點E為BC的中點,點P為BD上一動點,則PE+PC的最小值為( )
如圖,已知等邊△ABC的邊長為8,點D為AC的中點,點E為BC的中點,點P為BD上一動點,則PE+PC的最小值為( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 由題意可知點A、點C關于BD對稱,連接AE交BD于點P,由對稱的性質可得,PA=PC,故PE+PC=AE,由兩點之間線段最短可知,AE即為PE+PC的最小值.
解答 解:∵△ABC是等邊三角形,點D為AC的中點,點E為BC的中點,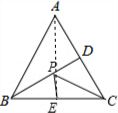
∴BD⊥AC,EC=4,
連接AE,線段AE的長即為PE+PC最小值,
∵點E是邊BC的中點,
∴AE⊥BC,
∴AE=$\sqrt{A{C}^{2}-E{C}^{2}}=\sqrt{{8}^{2}-{4}^{2}}=4\sqrt{3}$,
∴PE+PC的最小值是4$\sqrt{3}$.
故選D
點評 本題考查的是軸對稱-最短路線問題,熟知等邊三角形的性質是解答此題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
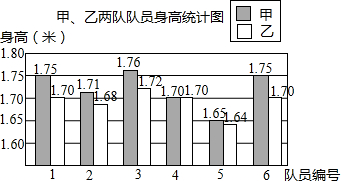 某校要成立一支由6名女生組成的舞蹈隊,初三(1)、(2)班各選6名女生,分別組成甲隊和乙隊參加選拔,每位女生的身高(cm)統計如圖,部分統計量如表:(單位:米)
某校要成立一支由6名女生組成的舞蹈隊,初三(1)、(2)班各選6名女生,分別組成甲隊和乙隊參加選拔,每位女生的身高(cm)統計如圖,部分統計量如表:(單位:米) | 平均數 | 標準差 | 中位數 | |
| 甲隊 | 1.72 | 0.038 | 1.73 |
| 乙隊 | 1.69 | 0.025 | 1.70 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
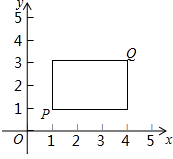 在平面直角坐標系xOy中,點P的坐標為(x1,y1),點Q的坐標為(x2,y2),且x1≠x2,y1≠y2,若P,Q為某個矩形的兩個頂點,且該矩形的邊均與某條坐標軸垂直,則稱該矩形為點P,Q的“相關矩形”,如圖為點P,Q的“相關矩形”示意圖.
在平面直角坐標系xOy中,點P的坐標為(x1,y1),點Q的坐標為(x2,y2),且x1≠x2,y1≠y2,若P,Q為某個矩形的兩個頂點,且該矩形的邊均與某條坐標軸垂直,則稱該矩形為點P,Q的“相關矩形”,如圖為點P,Q的“相關矩形”示意圖.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
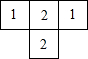 由6個小立方體組成的幾何體的俯視圖如圖1所示,每個小正方形上的數字表示該位置上擺放的小立方體的個數,則該幾何體的左視圖應為( )
由6個小立方體組成的幾何體的俯視圖如圖1所示,每個小正方形上的數字表示該位置上擺放的小立方體的個數,則該幾何體的左視圖應為( )| A. | 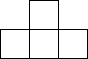 | B. | 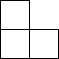 | C. | 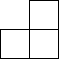 | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com