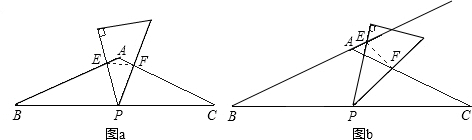
(1)證明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(兩角對應相等的兩個三角形相似).
(2)解:①△BPE∽△CFP;
②△BPE與△PFE相似.
下面證明結論:
同(1),可證△BPE∽△CFP,得

=

,而CP=BP,因此

.
又因為∠EBP=∠EPF,所以△BPE∽△PFE(兩邊對應成比例且夾角相等的兩個三角形相似).
③由②得△BPE∽△PFE,所以∠BEP=∠PEF.

分別過點P作PM⊥BE,PN⊥EF,垂足分別為M、N,則PM=PN.
連AP,在Rt△ABP中,由∠B=30°,AB=8,可得AP=4.
所以PM=2

,所以PN=2

,
所以s=

PN×EF=

m.
分析:(1)找出△BPE與△CFP的對應角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,從而解決問題;
(2)①小題同前可證,②小題可通過對應邊成比例證明,③小題求出△BPE中BE上的高,求出△PEF中EF上的高,得出關系式.
點評:這是一道操作探究題,它改變了多年來揚州市最后一道壓軸題以二次函數為主線的呈現方式.它以每位學生都有的30°三角板在圖形上的運動為背景,既考查了學生圖形旋轉變換的思想,靜中思動,動中求靜的思維方法,又考查了學生動手實踐、自主探究的能力.
問題的設置以問題串的形式呈現,層層推進,第1問入手容易,第2問深入困難,有一定的區分度,使不同層次的學生有不同的收獲.
同時通過本題的解答,一使同學們領悟到學習數學的方法,二是提醒教師學生在平時的教學中要注意變式練習.
本題的第1問不難,用兩角相等即可證得相似,第2問中的①由第1問類比即得,②要用到①中對應邊成比例代換后方可證得,③一般學生都能想到作高,卻想不到求這條高要用到角平分線、解直角三角形等知識.
實際上三角板運動到特殊位置還有一些結論,感興趣的學生不妨繼續研究.
要關注幾何圖形在運動狀態下幾何關系的不變性哦!

 =
= ,而CP=BP,因此
,而CP=BP,因此 .
.
 ,所以PN=2
,所以PN=2 ,
, PN×EF=
PN×EF= m.
m.

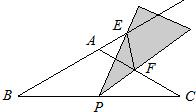 等腰△ABC,AB=AC,∠BAC=120°,P為BC上的中點,小慧拿著含30°角的透明三角板,使30°角的頂點落在點P處,三角板繞點P旋轉到如圖所示情形時,三角板的兩邊分別交BA的延長線于點E,交邊AC于點F,連接EF,△BPE與△PFE是否相似?請說明理由.
等腰△ABC,AB=AC,∠BAC=120°,P為BC上的中點,小慧拿著含30°角的透明三角板,使30°角的頂點落在點P處,三角板繞點P旋轉到如圖所示情形時,三角板的兩邊分別交BA的延長線于點E,交邊AC于點F,連接EF,△BPE與△PFE是否相似?請說明理由.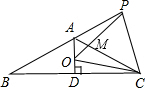 如圖,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,OP與AC相交與點M,則下列結論:
如圖,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,OP與AC相交與點M,則下列結論: