考點:勾股定理的逆定理
專題:證明題
分析:利用已知條件求出a=16,或b=16,或c=16,由a+b+c=32,得出b+c=a,或a+c=b,或a+b=c,根據勾股定理的逆定理即可證明以
,
,
為三邊長可構成一個直角三角形.
解答:
證明:將①代入②,得
+
+
=
,
兩邊同乘abc,整理得,1024-2(a
2+b
2+c
2)=
abc ③,
由①得(a+b+c)
2=1024,即a
2+b
2+c
2=1024-2(ab+bc+ca),
代入③,得1024-2[1024-2(ab+bc+ca)]=
abc,
即abc=16(ab+bc+ca)-4096,
(a-16)(b-16)(c-16)=abc-16(ab+bc+ca)+256(a+b+c)-16
3=-4096+256×32-16
3=0,
所以a=16,或b=16,或c=16,
∵a+b+c=32,
∴b+c=a,或a+c=b,或a+b=c,
∴以
,
,
為三邊長可構成一個直角三角形.
點評:本題考查了勾股定理的逆定理:如果三角形的三邊長a,b,c滿足a2+b2=c2,那么這個三角形就是直角三角形.同時考查了分式的運算,求出a=16,或b=16,或c=16是解題的關鍵.本題的計算難度較大.



 小學能力測試卷系列答案
小學能力測試卷系列答案 如圖,已知∠1=∠2,∠5=∠6,∠3=∠4,試說明AE∥BC,AE∥BD.請完成下列證明過程.
如圖,已知∠1=∠2,∠5=∠6,∠3=∠4,試說明AE∥BC,AE∥BD.請完成下列證明過程. 如圖,在正方形方格中,陰影部分是涂黑7個小正方形所形成的圖案,再將方格內空白的一個小正方形涂黑,使得到的新圖案成為一個軸對稱圖形的涂法有( )
如圖,在正方形方格中,陰影部分是涂黑7個小正方形所形成的圖案,再將方格內空白的一個小正方形涂黑,使得到的新圖案成為一個軸對稱圖形的涂法有( )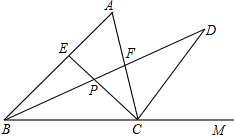 如圖所示,在△ABC中∠A=60°,∠ABC的角平分線和∠ACB的外角平分線交于點D,與∠ACB的角平分線交于點P,與邊AC交于點F.
如圖所示,在△ABC中∠A=60°,∠ABC的角平分線和∠ACB的外角平分線交于點D,與∠ACB的角平分線交于點P,與邊AC交于點F.