
分析 (1)分三種情況:①購進甲、乙型號洗衣機,②購進甲、丙型號洗衣機,③購進乙、丙型號洗衣機;根據(jù)“兩種不同型號的洗衣機50臺,共付48000元”列方程組求解可得;
(2)在(1)中所列方案中,根據(jù)“總利潤=兩種型號洗衣機的利潤和”列式計算,比較后即可得.
解答 解:(1)①當購進甲洗衣機x臺、乙洗衣機y臺,
根據(jù)題意得$\left\{\begin{array}{l}{x+y=50}\\{900x+1000y=48000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$;
②當購進甲洗衣機m臺、丙洗衣機n臺,
根據(jù)題意得:$\left\{\begin{array}{l}{m+n=50}\\{900m+1200n=48000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=40}\\{n=10}\end{array}\right.$;
③當購進乙洗衣機p臺,丙洗衣機q臺,
根據(jù)題意得:$\left\{\begin{array}{l}{p+q=50}\\{1000p+1200q=48000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{p=60}\\{q=-10}\end{array}\right.$(不符合實際意義,舍去);
故商場的購進方案有兩種:①購進甲洗衣機20臺、乙洗衣機30臺;②購進甲洗衣機40臺、丙洗衣機10臺;
(2)若購進甲洗衣機20臺、乙洗衣機30臺,
獲取的利潤為20×100+30×120=5600(元);
若購進甲洗衣機40臺、丙洗衣機10臺,
獲取的利潤為40×100+10×140=5400(元);
∵5600>5400,
∴購進甲洗衣機20臺、乙洗衣機30臺獲取的利潤較大.
點評 本題主要考查二元一次方程組的應用,根據(jù)題意分類討論,并依據(jù)相等關系列出方程組是解題的關鍵.


科目:初中數(shù)學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 在一次運輸任務中,一輛汽車將一批貨物從深圳運往廣州,到達廣州卸貨后返回,設汽車從深圳出發(fā)x(h)時,汽車與深圳的距離為y(km),y與x的函數(shù)關系如圖所示.根據(jù)圖象信息,解答下列問題:
在一次運輸任務中,一輛汽車將一批貨物從深圳運往廣州,到達廣州卸貨后返回,設汽車從深圳出發(fā)x(h)時,汽車與深圳的距離為y(km),y與x的函數(shù)關系如圖所示.根據(jù)圖象信息,解答下列問題:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
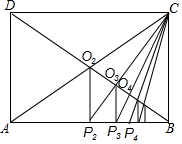 在美國的一堂數(shù)學課上,老師給同學們布置了一道“任意等分一條線段”的題.其中有一個學生用了一種與眾不同的方法.他在紙上做出了如圖所示的一個圖形,他以老師給的已知線段AB為一條邊作矩形ABCD,設AC、BD交于點O2,作O2P2⊥AB,則垂足P2就是AB的二等分點:連接CP2交BD于點O3,作O3P3⊥AB,則垂足P3就是AB的三等分點;再依次做下去,就得到AB的四等分點,…n等分點.你能用所學過的知識解釋其中的緣由嗎?
在美國的一堂數(shù)學課上,老師給同學們布置了一道“任意等分一條線段”的題.其中有一個學生用了一種與眾不同的方法.他在紙上做出了如圖所示的一個圖形,他以老師給的已知線段AB為一條邊作矩形ABCD,設AC、BD交于點O2,作O2P2⊥AB,則垂足P2就是AB的二等分點:連接CP2交BD于點O3,作O3P3⊥AB,則垂足P3就是AB的三等分點;再依次做下去,就得到AB的四等分點,…n等分點.你能用所學過的知識解釋其中的緣由嗎?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | -3噸 | B. | +3噸 | C. | -5噸 | D. | +5噸 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com