
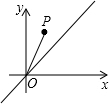
 如圖,在平面直角坐標(biāo)系中,點(diǎn)P的坐標(biāo)為(1,2),將線段OP沿y軸正方向移動m(m>0)個單位長度至O′P′,以O(shè)′P′為直角邊在第一象限內(nèi)作等腰直角△O′P′Q,若點(diǎn)Q在直線y=x上,則m的值為2或3.
如圖,在平面直角坐標(biāo)系中,點(diǎn)P的坐標(biāo)為(1,2),將線段OP沿y軸正方向移動m(m>0)個單位長度至O′P′,以O(shè)′P′為直角邊在第一象限內(nèi)作等腰直角△O′P′Q,若點(diǎn)Q在直線y=x上,則m的值為2或3. 分析 以O(shè)′P′為直角邊在第一象限內(nèi)作等腰直角△O′P′Q,需要分兩種情況進(jìn)行討論,先根據(jù)等腰直角三角形的性質(zhì),判定全等三角形,再根據(jù)全等三角形的性質(zhì),得出對應(yīng)邊相等,最后根據(jù)線段的和差關(guān)系以及平移的方向,得出平移的距離即可.
解答  解:①如圖所示,當(dāng)△O′P′Q為等腰直角三角形時,過點(diǎn)P'作P'A⊥y軸于A,過Q作QB⊥y軸于B,則
解:①如圖所示,當(dāng)△O′P′Q為等腰直角三角形時,過點(diǎn)P'作P'A⊥y軸于A,過Q作QB⊥y軸于B,則
∠O'AP'=90°=∠QBO',∠P'O'Q=90°,
∴∠AO'P'+∠BO'Q=90°=∠O'QB+∠BO'Q,
∴∠AO'P'=∠O'QB,
又∵O'P'=QO',
∴△O'AP'≌△QBO',
∴AP'=BO',AO'=BQ,
∵點(diǎn)P的坐標(biāo)為(1,2),
∴由平移可得,AP'=1,AO'=2,
∴BO'=1,
當(dāng)點(diǎn)Q在直線y=x上時,BQ=2=BO,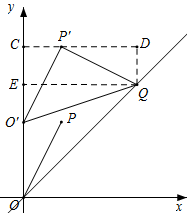
此時OO'=BO'+BO=1+2=3,
即平移的距離m為3;
②如圖所示,過點(diǎn)P'作x軸的平行線交y軸于C,過點(diǎn)Q作y軸的平行線,交直線CP'于點(diǎn)D,
過點(diǎn)Q作QE⊥y軸于E,
同理可得,△O'CP'≌△P'DQ,
∴CE=DQ=CP'=1,DP'=CO'=2,
∴CD=EQ=1+2=3=OE,EO'=CO'-CE=2-1=1,
∴OO'=OE-O'E=3-1=2,
即平移的距離m為2,
故答案為:2或3.
點(diǎn)評 本題主要考查了全等三角形的判定與性質(zhì),等腰直角三角形的性質(zhì)以及平移的性質(zhì),解決問題的關(guān)鍵是根據(jù)圖形進(jìn)行分類討論,運(yùn)用全等三角形的對應(yīng)邊相等進(jìn)行計算求解.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,經(jīng)過點(diǎn)B(1,0)的直線y=kx+b與直線y=4x+4相交于點(diǎn)A(m,$\frac{8}{3}$),則0<kx+b<4x+4的解集為( )
如圖,經(jīng)過點(diǎn)B(1,0)的直線y=kx+b與直線y=4x+4相交于點(diǎn)A(m,$\frac{8}{3}$),則0<kx+b<4x+4的解集為( )| A. | x<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<x<1 | C. | x<1 | D. | -1<x<1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
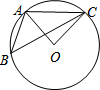 如圖,點(diǎn)A、B、C均在⊙O上,若∠ABC=40°,則∠AOC的大小是( )
如圖,點(diǎn)A、B、C均在⊙O上,若∠ABC=40°,則∠AOC的大小是( )| A. | 90° | B. | 80° | C. | 70° | D. | 50° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | p(1+10%)萬元 | B. | (p+10%)萬元 | C. | $\frac{p}{1+10%}$萬元 | D. | $\frac{p}{1-10%}$萬元 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com