
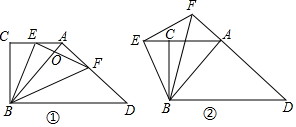
分析 (1)根據三角形內角和定理以及對頂角相等即可得出結論;
(2)過E作EM⊥AE交AB于M,先判定△AFE≌△MBE(AAS),得出EF=EB,∠FEA=∠BEM,進而得到∠BEF=∠MEA=90°,即可得出△BEF為等腰直角三角形;
(3)過E作EM⊥AE交AB延長線于點M,先判定△EBM≌△EFA(AAS),得出EB=EF,∠FEA=∠BEM,即可得到∠BEF=∠MEA=90°,進而得出△BEF為等腰直角三角形.
解答 解:(1)證明:∵EF⊥EB,
∴∠FEB=90°=∠BAF,
∵∠AFE=90°-∠AOF,∠ABE=90°-∠BOE,
而∠EOB=∠AOF,
∴∠AFE=∠ABE;
(2)△EBF為等腰直角三角形,
證明:如圖1,過E作EM⊥AE交AB于M,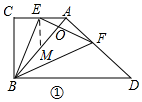
在等腰直角三角形ABC中,∠BAC=45°,
∴∠EAM=∠AME=45°,
∴EA=EM,
∵∠FAE=45°+90°=135°,∠EMB=180°-45°=135°,
∴∠FAE=∠EMB,
在△AEP和△MBP中,
$\left\{\begin{array}{l}{∠FAE=∠EMB}\\{∠AFE=∠EBM}\\{AE=ME}\end{array}\right.$,
∴△AFE≌△MBE(AAS),
∴EF=EB,∠FEA=∠BEM,
∴∠BEF=∠MEA=90°,
∴△BEF為等腰直角三角形;
(3)△BEF為等腰直角三角形仍成立.
證明:如圖2,過E作EM⊥AE交AB延長線于點M,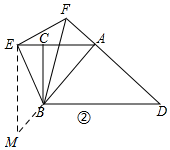
易得∠EMB=∠EAB=45°=∠EAF,
∴EM=EA,
∵∠FEB+∠FAB=90°+90°=180°,
∴∠EFA+∠ABE=180°,
又∵∠EBM+∠EBA=180°,
∴∠EBM=∠EFA,
在△EBM和△EFA中,
$\left\{\begin{array}{l}{∠EMB=∠EAF}\\{∠EBM=∠EFA}\\{ME=AE}\end{array}\right.$,
∴△EBM≌△EFA(AAS),
∴EB=EF,∠FEA=∠BEM,
∴∠BEF=∠MEA=90°,
∴△BEF為等腰直角三角形.
點評 本題屬于三角形綜合題,主要考查了全等三角形的判定與性質以及等腰直角三角形的性質的綜合應用,解決問題的關鍵是作輔助線構造全等三角形,根據全等三角形的對應邊相等進行求解.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:初中數學 來源: 題型:選擇題
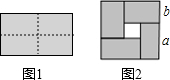 如圖1是一個長為2a,寬為2b(a>b)的長方形,用剪刀沿圖中虛線(對稱軸)剪開,把它分成四塊形狀和大小都一樣的小長方形,然后按圖2那樣拼成一個正方形,則中間空的部分的面積( )
如圖1是一個長為2a,寬為2b(a>b)的長方形,用剪刀沿圖中虛線(對稱軸)剪開,把它分成四塊形狀和大小都一樣的小長方形,然后按圖2那樣拼成一個正方形,則中間空的部分的面積( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=kx+b與反比例函數y=$\frac{a}{x}$在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
如圖,一次函數y=kx+b與反比例函數y=$\frac{a}{x}$在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com