
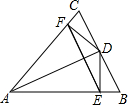
 如圖,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F分別為垂足,則下列四個結論:(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF;(4)AD垂直平分EF.其中正確的有( )
如圖,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F分別為垂足,則下列四個結論:(1)∠DEF=∠DFE;(2)AE=AF;(3)AD平分∠EDF;(4)AD垂直平分EF.其中正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 根據角平分線的性質和等腰三角形的形狀可得正確;根據全等三角形對應邊相等可得AE=AF,∠ADE=∠ADF可得②③正確;
解答 解:∵AB=AC,
∴△ABC是等腰三角形,∠B=∠C.
∵AD平分∠BAC,
∴BD=CD,
∵DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴∠DEF=∠DFE,故①正確;
在Rt△ADE和Rt△ADF中,
$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,故②③正確;
∵AE=AF,AD平分∠BAC,
∴AD垂直平分EF,故④正確;
故選D.
點評 本題考查了等腰三角形三線合一的性質,全等三角形的判定與性質,角平分線上的點到角的兩邊的距離相等,線段垂直平分線上的點到線段兩端點的距離相等的性質,綜合題,但難度不大,熟記各性質是解題的關鍵.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,點D在AB上一點,下列條件中,能使△ABC與△BDC相似的是( )
如圖,在△ABC中,點D在AB上一點,下列條件中,能使△ABC與△BDC相似的是( )| A. | ∠B=∠ACD | B. | ∠ACB=∠ADC | C. | AC2=AD•AB | D. | BC2=BD•AB |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
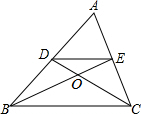 如圖,在△ABC中,D,E分別是AB,AC的中點,BE,CD相交于點O,△DOE與△COB的面積比為( )
如圖,在△ABC中,D,E分別是AB,AC的中點,BE,CD相交于點O,△DOE與△COB的面積比為( )| A. | 1:4 | B. | 2:3 | C. | 1:3 | D. | 1:2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 暑假期間,小明的媽媽趁電器打價格戰之機在網上購買了一臺電視,小明量了電視機的屏幕后,發現屏幕93厘米長和52厘米寬,則這臺電視機為________英寸(實際測量的誤差可不計)( )
暑假期間,小明的媽媽趁電器打價格戰之機在網上購買了一臺電視,小明量了電視機的屏幕后,發現屏幕93厘米長和52厘米寬,則這臺電視機為________英寸(實際測量的誤差可不計)( )| A. | 32(81厘米) | B. | 39(99厘米) | C. | 42(106厘米) | D. | 46(117厘米) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com