
【題目】如圖所示已知![]() ,
,![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ;
;
(1)![]() ;
;
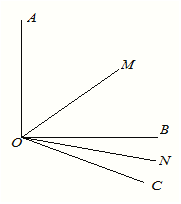
(2)如圖∠AOB=900,將OC繞O點向下旋轉,使∠BOC=![]() ,仍然分別作∠AOC,∠BOC的平分線OM,ON,能否求出∠MON的度數,若能,求出其值,若不能,試說明理由.
,仍然分別作∠AOC,∠BOC的平分線OM,ON,能否求出∠MON的度數,若能,求出其值,若不能,試說明理由.

(3)![]() ,
,![]() ,仍然分別作∠AOC,∠BOC的平分線OM,ON,能否求出∠MON的度數,若能,求
,仍然分別作∠AOC,∠BOC的平分線OM,ON,能否求出∠MON的度數,若能,求![]() 的度數;并從你的求解中看出什么什么規律嗎?
的度數;并從你的求解中看出什么什么規律嗎?

【答案】(1)![]() ;
;
(2)能,因為∠AOB=900,∠BOC=![]() , 所以∠AOC=900+
, 所以∠AOC=900+![]() ,
,
因為OM、 ON平分∠AOC,∠BOC的線
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (900+
(900+![]() )=450+x
)=450+x
所以∠CON=![]() ∠BOC=x
∠BOC=x
所以∠MON=∠MOC-∠CON=450+x-x=450
(3)能,因為∠AOB=![]() ,∠BOC=
,∠BOC=![]() ,
,
所以∠AOC=![]() +
+![]() ,
,
因為OM、 ON平分∠AOC,∠BOC的線
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (
(![]() +
+![]() )
)
所以∠CON=![]() ∠BOC=
∠BOC=![]()
![]()
所以∠MON=∠MOC-∠CON=![]() (
(![]() +
+![]() )-
)-![]()
![]() =
=![]()
![]()
即![]() .
.
【解析】
(1)根據題意可知,∠AOC=120°,由OM平分∠AOC,ON平分∠BOC;推出∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,由圖形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根據(1)的求解思路,先利用角平分線的定義表示出∠MOC與∠NOC的度數,然后相減即可得到∠MON的度數;(3)用α、β表示∠MOC,∠NOC,根據∠MON=∠MOC-∠NOC得到.
∠BOC=15°,由圖形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根據(1)的求解思路,先利用角平分線的定義表示出∠MOC與∠NOC的度數,然后相減即可得到∠MON的度數;(3)用α、β表示∠MOC,∠NOC,根據∠MON=∠MOC-∠NOC得到.
(1)(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOC-∠CON=60°-15°=45°;
故答案為:45;
(2)能.∵∠AOB=90°,∠BOC=2x°,
∴∠AOC=90°+2x°,
∵OM、ON分別平分∠AOC,∠BOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (90°+2x°)=45°+x,
(90°+2x°)=45°+x,
∴∠CON=![]() ∠BOC=x,
∠BOC=x,
∴∠MON=∠MOC-∠CON=45°+x-x=45°
(3))∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (α+β)-
(α+β)-![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】某收費站在2小時內對經過該站的機動車統計如下:
類型 | 轎車 | 貨車 | 客車 | 其他 |
數量(輛) | 36 | 24 | 8 | 12 |
若有一輛機動車將經過這個收費站,利用上面的統計估計它是轎車的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰△ABC中,AC=BC,以BC為直徑的⊙O分別與AB,AC相交于點D,E,過點D作DF⊥AC,垂足為點F. 
(1)求證:DF是⊙O的切線;
(2)分別延長CB,FD,相交于點G,∠A=60°,⊙O的半徑為6,求陰影部分的面積. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】尺規作圖特有的魅力曾使無數人沉湎其中,連當年叱咤風云的拿破侖也不例外,我們可以只用圓規將圓等分.例如可將圓6等分,如圖只需在⊙O上任取點A,從點A開始,以⊙O的半徑為半徑,在⊙O上依次截取點B,C,D,E,F.從而點A,B,C,D,E,F把⊙O六等分.下列可以只用圓規等分的是( ) ①兩等分 ②三等分 ③四等分 ④五等分.
A.②
B.①②
C.①②③
D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有甲、乙兩個瓷器店出售茶壺和茶杯,茶壺每只價格為20元,茶杯每只價格為5元,已知甲店制定的優惠方法是買一只茶壺送一只茶杯,乙店按總價的92%付款.學校辦公室需要購買茶壺4只,茶杯若干只(不少于4只).
(1)當購買多少只茶杯時,兩店的優惠方法付款一樣多?
(2)當需要購買40只茶杯時,若讓你去辦這件事,你打算去哪家商店購買?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一張長方形紙片ABCD沿EF折疊后ED與BC的交點為G,D、C分別在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度數;
(2)∠FEG的度數;
(3)∠1和∠2的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,已知AD是角平分線,∠B=66°,∠C=54°.
(1)求∠ADB的度數;
(2)若DE⊥AC于點E,求∠ADE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x+2)(x2-4x+6)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式
B.平方差公式
C.兩數和的完全平方公式
D.兩數差的完全平方公式
(2)該同學因式分解的結果是否徹底?________.(填“徹底”或“不徹底”)
若不徹底,請直接寫出因式分解的最后結果_________.
(3)請你模仿以上方法嘗試對多項式(x2-2x)(x2-2x+2)+1進行因式分解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
① ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
…
(1)請按以上規律寫出第⑤個等式:;
(2)猜想并寫出第n個等式:;
(3)請證明猜想的正確性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com