
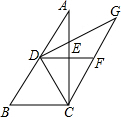
 如圖,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延長線于點F.
如圖,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延長線于點F.分析 (1)首先證明四邊形DBCF為平行四邊形,可得DF=BC,再證明DE=$\frac{1}{2}$BC,進而得到EF=$\frac{1}{2}$CB,即可證出DE=EF;
(2)首先畫出圖形,首先根據平行線的性質可得∠ADG=∠G,再證明∠B=∠DCB,∠A=∠DCA,然后再推出∠1=∠DCB=∠B,再由∠A+∠ADG=∠1可得∠A+∠G=∠B.
解答 證明:(1)∵DE∥BC,CF∥AB,
∴四邊形DBCF為平行四邊形,
∴DF=BC,
∵D為邊AB的中點,DE∥BC,
∴DE=$\frac{1}{2}$BC,
∴EF=DF-DE=BC-$\frac{1}{2}$CB=$\frac{1}{2}$CB,
∴DE=EF;
(2)∵DB∥CF,
∴∠ADG=∠G,
∵∠ACB=90°,D為邊AB的中點,
∴CD=DB=AD,
∴∠B=∠DCB,∠A=∠DCA,
∵DG⊥DC,
∴∠DCA+∠DEC=90°,
∵∠DCB+∠DCA=90°,
∴∠DEC=∠DCB=∠B,
∵∠A+∠ADG=∠DEC,
∴∠B=∠A+∠DGC.
點評 此題主要考查了平行四邊形的判定與性質,以及直角三角形的性質,關鍵是找出∠ADG=∠G,∠1=∠B.掌握在直角三角形中,斜邊上的中線等于斜邊的一半.


科目:初中數學 來源: 題型:選擇題
| A. | 11×103 | B. | 0.11×105 | C. | 1.1×103 | D. | 1.1×104 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
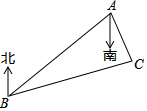 如圖,C島在A島的南偏東15°方向,C島在B島的北偏東70°方向,從C島看A、B兩島的視角∠ACB的度數是( )
如圖,C島在A島的南偏東15°方向,C島在B島的北偏東70°方向,從C島看A、B兩島的視角∠ACB的度數是( )| A. | 95° | B. | 85° | C. | 60° | D. | 40° |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
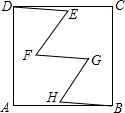 如圖,在正方形ABCD中,點E,F,G,H均在其內部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,則AB=$\sqrt{7}$.
如圖,在正方形ABCD中,點E,F,G,H均在其內部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,則AB=$\sqrt{7}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
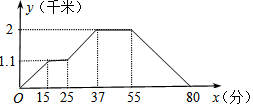 如圖,小強從家去菜地澆水,又去玉米地除草,然后回家.其中x表示時間,y表示小強離他家的距離,小強家、菜地、玉米地在同一直線上.如果菜地和玉米地的距離為a千米,小強從玉米地回家的平均速度為b千米/分,則a、b的值分別為( )
如圖,小強從家去菜地澆水,又去玉米地除草,然后回家.其中x表示時間,y表示小強離他家的距離,小強家、菜地、玉米地在同一直線上.如果菜地和玉米地的距離為a千米,小強從玉米地回家的平均速度為b千米/分,則a、b的值分別為( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com