
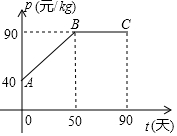
 某公司購進一種商品的成本為30元/kg,經市場調研發現,這種商品在未來90
某公司購進一種商品的成本為30元/kg,經市場調研發現,這種商品在未來90| 時間t(天) | 10 | 30 |
| 每天的銷售量 y(kg) | 180 | 140 |
分析 (1)直接利用待定系數法求出一次函數解析式,進而得出答案;
(2)利用銷量×每千克利潤=總利潤,進而求出答案;
(3)利用二次函數增減性結合對稱軸公式得出n的取值范圍.
解答 解:(1)設y=kt+b,把t=10,y=180;t=30,y=140代入得到:
$\left\{\begin{array}{l}{10k+b=180}\\{30k+b=140}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$,
∴y=-2t+200.
當0<t<50時,設p=kt+40,由圖象得B(50,90)
∴50k+40=90,
∴k=1,
∴p=t+40,
當50≤t≤90時,p=90;
(2)由題意可得:w=(-2t+200)(t+40-30)
=-2t2+180t+2000
=-2(t-45)2+6050,
∴t=45時,w最大值為6050元,
w=(-2t+120)(90-30)=-120t+12000,
∵-120<0,
∴w隨x增大而減小,
∴t=50時,w最大值=6000,
綜上所述第45天利潤最大,最大利潤為6050元;
(3)設前50天每天扣除捐贈后的日銷售利潤為m元.
由題意m=-2t2+180t+2000-(-2t+200)n
=-2t2+(180+2n)t+2000-200n,
∵在前50天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,
∴-$\frac{b}{2a}$=-$\frac{180+2n}{-4}$≥50,
∴n≥10.
又∵n<12,
∴n的取值范圍為:10≤n<12.
點評 此題主要考查了二次函數的應用,熟練掌握各函數的性質和圖象特征,最值問題需由函數的性質求解時,正確表達關系式是關鍵.


科目:初中數學 來源: 題型:解答題
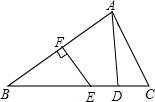 如圖,在△ABC中,AB的垂直平分線EF交BC于點E,交AB于點F,D為線段CE的中點,BE=AC.
如圖,在△ABC中,AB的垂直平分線EF交BC于點E,交AB于點F,D為線段CE的中點,BE=AC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
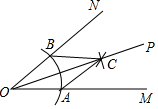 如圖,用尺規作∠MON的平分線OP.由作圖知△OAC≌△OBC,從而得OP平分∠MON,則此兩個三角形全等的依據是( )
如圖,用尺規作∠MON的平分線OP.由作圖知△OAC≌△OBC,從而得OP平分∠MON,則此兩個三角形全等的依據是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 測量該四邊形的對角線是否互相垂直 | |
| B. | 測量該四邊形的對角線是否相等 | |
| C. | 測量該四邊形的對角線是否互相平分 | |
| D. | 測量該四邊形的四條邊是否都相等 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com