Question

4．如圖①，邊長為a的正方形發生形變后成為邊長為a的菱形，如果這個菱形的一組對邊之間的距離為h，我們把$\frac{a}{h}$的比值叫做這個菱形的“形變度”．
（Ⅰ）當形變后的菱形有一個內角是60°時，則這個菱形的“形變度”為$\frac{2\sqrt{3}}{3}$．
（Ⅱ）如圖②，正方形ABCD由16個邊長為1的小正方形組成，形變后成為菱形A′B′C′D′，△AEF（E、F是小正方形的頂點）同時形變為△A′E′F′，設這個菱形的“形變度“為k，△A′E′F′的面積為S，當$\frac{A′C′}{B′D′}$=$\frac{4k}{3}$時，S的值等于$\frac{8\sqrt{2}}{3}$．

Answer 1

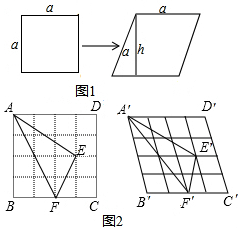
分析 （Ⅰ）用“形變度”的定義直接計算即可；
（Ⅱ）先確定出S與k的函數關系式，用形變度和菱形的面積求解即可．

解答 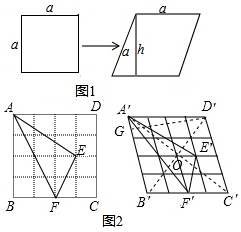解：（Ⅰ）由題意得，sin60°=$\frac{h}{a}$=$\frac{\sqrt{3}}{2}$，
∴$\frac{a}{h}$=$\frac{2\sqrt{3}}{3}$；                                            
故答案為$\frac{2\sqrt{3}}{3}$，
（Ⅱ）如圖，過D′作D′G⊥A′B′，垂足為G，A′C′與B′D′相交于O，
則$\frac{A′D′}{D′G}$=k，
∵A′B′=B′C′=C′D′=A′D′=4，
∴D'G=$\frac{4}{k}$，
∵S_△AEF=3×4-$\frac{1}{2}×$2×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3=4，
∵這個菱形的“形變度“為k，
∴△A′E′F′的形變度“為k，
∴S=$\frac{4}{k}$，
∴S是k的反比例函數．                                          
當 $\frac{A′C′}{B′D′}$=$\frac{4k}{3}$時，$\frac{\frac{1}{2}A′C′}{\frac{1}{2}B′D′}$=$\frac{4k}{3}$，
∴$\frac{A′O}{D′O}$=$\frac{4k}{3}$，
設A′O=4kt，D′O=3t，
∴（4kt）²+（3t）²=16，
∴t²=$\frac{16}{16k+9}$，
∴S_菱形ABCD=$\frac{1}{2}$A′C′•B′D′=$\frac{16}{k}$，
∴$\frac{1}{2}$×8kt×6t=$\frac{16}{k}$，
即24kt²=$\frac{16}{k}$，
∴k=$\frac{3\sqrt{2}}{4}$．
∴S=$\frac{8\sqrt{2}}{3}$．
故答案為：$\frac{8\sqrt{2}}{3}$．

點評 此題是四邊形綜合題，主要考查了新定義，圖形形變前后的圖形的形狀，面積的計算，勾股定理，解本題的關鍵是理解新定義．